1. (数形结合)涂一涂,填一填。
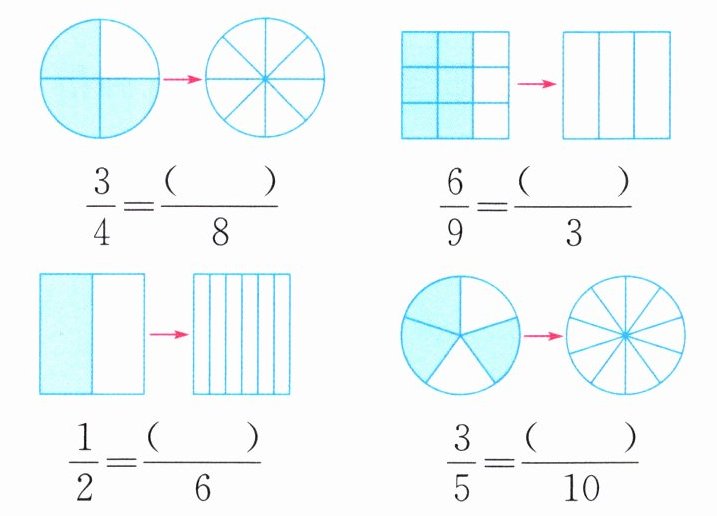
答案:1.涂6格 6 涂2格 2 涂3格 3 涂6格 6
解析:
涂6格 $\frac{3}{4}=\frac{6}{8}$ 涂2格 $\frac{6}{9}=\frac{2}{3}$ 涂3格 $\frac{1}{2}=\frac{3}{6}$ 涂6格 $\frac{3}{5}=\frac{6}{10}$
(1) 在括号里填合适的数。
$ \frac{(\ \ \ \ \ \ )}{64} = \frac{6}{8} = \frac{3}{(\ \ \ \ \ \ )} = \frac{12}{(\ \ \ \ \ \ )} = \frac{(\ \ \ \ \ \ )}{32} $
$ (\ \ \ \ \ \ ) ÷ 56 = \frac{28}{(\ \ \ \ \ \ )} = \frac{4}{7} = \frac{(\ \ \ \ \ \ )}{21} = \frac{36}{(\ \ \ \ \ \ )} $
答案:2.(1)48 4 16 24 32 49 12 63
解析:
48;4;16;24;32;49;12;63
$(2) $把$ \frac{7}{10} $的分子乘$ 3,$要使分数的大小不变$,$分母要乘$($
$3$
$)。$
答案:2.(2)3
$(3) \frac{45}{81} $的分母除以$ 9,$要使分数的大小不变$,$分子应除以$($
$9$
$)$或减少$($
$40$
$)。$
答案:2.(3)9 40
$(4) $一个分数的分子、分母先同时除以$ 2,$再同时乘$ 8 $后得
到
$ \frac{32}{24} ,$原来这个分数是$($
$\frac{8}{6}$
$)。$
答案:$2.(4)\frac{8}{6}$
解析:
$\frac{32}{24}÷8×2=\frac{4}{3}×2=\frac{8}{6}$
3. 下面哪些分数在直线上能用同一个点表示? 把这些分数在直线上表示出来。
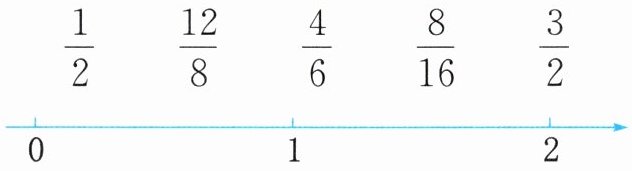
答案: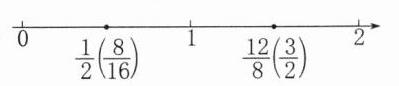
解析:
$\frac{1}{2}=\frac{8}{16}$,$\frac{12}{8}=\frac{3}{2}$
在直线上,$\frac{1}{2}$和$\frac{8}{16}$用同一个点表示,$\frac{12}{8}$和$\frac{3}{2}$用同一个点表示。
表示如下:0,$\frac{1}{2}(\frac{8}{16})$,1,$\frac{12}{8}(\frac{3}{2})$,2
(1) 下面各组分数中,不相等的是(
C
)。
$A.\frac{4}{7} $和$ \frac{12}{21} $
$B.\frac{35}{5} $和$ \frac{42}{6}$
$C.1 \frac{2}{3} $和$ 2 \frac{6}{9} $
$D.\frac{60}{8} $和$ \frac{30}{4} $
答案:4.(1)C
解析:
A. $\frac{12}{21}=\frac{12÷3}{21÷3}=\frac{4}{7}$,相等;
B. $\frac{35}{5}=7$,$\frac{42}{6}=7$,相等;
C. $1\frac{2}{3}=\frac{5}{3}=\frac{15}{9}$,$2\frac{6}{9}=\frac{24}{9}$,$\frac{15}{9}\neq\frac{24}{9}$,不相等;
D. $\frac{60}{8}=\frac{60÷2}{8÷2}=\frac{30}{4}$,相等。
C
$(2) \frac{7}{17} $的分子增加$ 21,$要使分数的大小不变$,$下面的说法不正确的是$($
$A$
$)。$
A.分母增加 21
B.分母增加 51
C.分母乘 4
D.分母增加 3 倍
答案:4.(2)A
解析:
原分数为$\frac{7}{17}$,分子增加21后变为$7 + 21=28$,$28÷7 = 4$,即分子扩大到原来的4倍。要使分数大小不变,分母也应扩大到原来的4倍,变为$17×4 = 68$。分母增加的值为$68-17 = 51$,增加的倍数为$(68 - 17)÷17=3$倍。选项A中分母增加21后为$17+21 = 38$,$\frac{28}{38}\neq\frac{7}{17}$,所以说法不正确的是A。
A
5. (说理表达)爸爸买了一个大西瓜,弟弟想多吃一些。爸爸说:“我吃$$ \frac{1}{5} $$,哥哥吃$$ \frac{2}{10} $$,你吃$$ \frac{3}{15} $$,剩下的给妈妈,怎么样?”弟弟一听满意极了。

答案:$5.\frac{1}{5}=\frac{2}{10}=\frac{3}{15} \frac{1}{5}+\frac{1}{5}+\frac{1}{5}=\frac{3}{5} 1-\frac{3}{5}=\frac{2}{5}$
$\frac{1}{5}<\frac{2}{5}$弟弟没有多吃,妈妈吃的最多。
$6. ($算理理解$)$在探究分数的基本性质时$,$奇奇说$:“$这无须质疑$,$我们可以将分数转化成除法证明$!”$
$ \frac{2}{3} = 2 ÷ 3 \ \ \ \ \ \ \ \ \ \ \ \ \frac{4}{6} = (\ \ \ \ \ \ ) ÷ 6 \ \ \ \ \ \ \ \ \ \ \ \ \frac{6}{9} = 6 ÷ (\ \ \ \ \ \ ) $
因为$ 2 ÷ 3 = (\ \ \ \ \ \ ) ÷ 6 = 6 ÷ (\ \ \ \ \ \ ) ,$
所以$ \frac{2}{3} = \frac{(\ \ \ \ \ \ )}{(\ \ \ \ \ \ )} = \frac{(\ \ \ \ \ \ )}{(\ \ \ \ \ \ )} 。$

答案:$6.4 9 4 9 \frac{4}{6}=\frac{6}{9} $商不变的规律
$7. ($思维过程$)$一个分数的分子加上$ 1,$结果是$ \frac{3}{4} ;$分子减去$ 1,$结果是$ \frac{1}{2} 。$这个分数是$($
$\frac{5}{8}$
$)。$
答案:$7.\frac{5}{8} $解析:把得到的两个分数化成同分母分数,
$\frac{3}{4}=\frac{6}{8},\frac{1}{2}=\frac{4}{8},\frac{6 - 1}{8}=\frac{4 + 1}{8},$所以原分数是$\frac{5}{8}。$