4. (2025·宿迁校级一模)如图甲所示,在容器底部固定一个轻质弹簧,在弹簧上端连有一棱长为 0.1 m 的实心正方体物块 A,当容器中水的深度为 20 cm 时,物块 A 有$\frac{3}{5}$的体积露出水面,此时弹簧恰好处于自然伸长状态。求:(已知水的密度为$1×10^{3}$ kg/$m^{3}$,g 取 10 N/kg)
(1) 物块 A 受到的浮力。
(2) 物块 A 的密度。
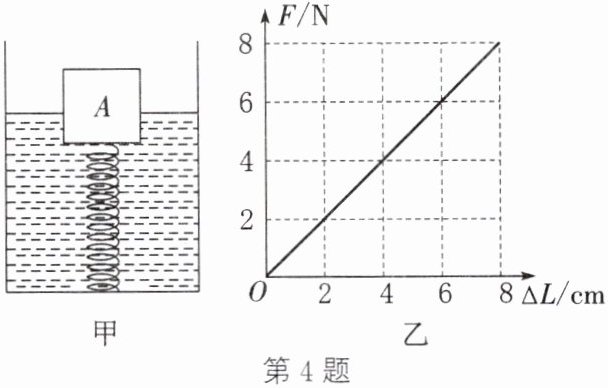
(3) 往容器中缓慢加水(水未溢出)至物块 A 恰好浸没时水面升高的高度(整个过程弹簧受到的拉力跟弹簧的伸长量的关系如图乙所示)。
解析:
(1) 物块$A$的体积$V=(0.1\,\mathrm{m})^{3}=1×10^{-3}\,\mathrm{m}^{3}$,排开水的体积$V_{\mathrm{排}}=V-\frac{3}{5}V=\frac{2}{5}V=\frac{2}{5}×1×10^{-3}\,\mathrm{m}^{3}=4×10^{-4}\,\mathrm{m}^{3}$,浮力$F_{\mathrm{浮}}=\rho_{\mathrm{水}}gV_{\mathrm{排}}=1×10^{3}\,\mathrm{kg/m}^{3}×10\,\mathrm{N/kg}×4×10^{-4}\,\mathrm{m}^{3}=4\,\mathrm{N}$。
(2) 弹簧自然伸长时物块漂浮,$G=F_{\mathrm{浮}}=4\,\mathrm{N}$,物块质量$m=\frac{G}{g}=\frac{4\,\mathrm{N}}{10\,\mathrm{N/kg}}=0.4\,\mathrm{kg}$,密度$\rho_{\mathrm{物}}=\frac{m}{V}=\frac{0.4\,\mathrm{kg}}{1×10^{-3}\,\mathrm{m}^{3}}=0.4×10^{3}\,\mathrm{kg/m}^{3}$。
(3) 物块浸没时浮力$F_{\mathrm{浮}}'=\rho_{\mathrm{水}}gV=1×10^{3}\,\mathrm{kg/m}^{3}×10\,\mathrm{N/kg}×1×10^{-3}\,\mathrm{m}^{3}=10\,\mathrm{N}$,弹簧拉力$F=F_{\mathrm{浮}}'-G=10\,\mathrm{N}-4\,\mathrm{N}=6\,\mathrm{N}$,由图乙得弹簧伸长量$\Delta L=6\,\mathrm{cm}$。初始时物块浸入深度$h_{\mathrm{浸}}=(1-\frac{3}{5})×10\,\mathrm{cm}=4\,\mathrm{cm}$,弹簧原长$L_{0}=20\,\mathrm{cm}-4\,\mathrm{cm}=16\,\mathrm{cm}$,浸没时弹簧长度$L'=16\,\mathrm{cm}+6\,\mathrm{cm}=22\,\mathrm{cm}$,水面高度$h_{2}=22\,\mathrm{cm}+10\,\mathrm{cm}=32\,\mathrm{cm}$,水面升高$\Delta h=32\,\mathrm{cm}-20\,\mathrm{cm}=12\,\mathrm{cm}$。
(1) $4\,\mathrm{N}$;(2) $0.4×10^{3}\,\mathrm{kg/m}^{3}$;(3) $12\,\mathrm{cm}$