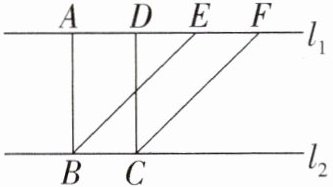
8. 如图,$l_1 // l_2$,$BE // CF$,$BA ⊥ l_1$,$DC ⊥ l_2$,下面给出四个结论:① $BE = CF$;② $AB = DC$;③ $S_{△ ABE} = S_{△ DCF}$;④四边形 $ABCD$ 是矩形。其中说法正确的有(
D
)
A.1 个
B.2 个
C.3 个
D.4 个
答案:8. D 解析:
∵ $ l _ { 1 } // l _ { 2 } $,$ BE // CF $,
∴ 四边形 $ BCFE $ 是平行四边形,
∴ $ BE = CF $,故 ① 正确;
∵ $ l _ { 1 } // l _ { 2 } $,$ BA ⊥ l _ { 1 } $,$ DC ⊥ l _ { 2 } $,
∴ $ AB = DC $,故 ② 正确;
∵ $ BE // CF $,
∴ $ ∠AEB = ∠DFC $. 在 $ △ABE $ 和 $ △DCF $ 中,$ \{ \begin{array} { l } { ∠AEB = ∠DFC, } \\ { ∠BAE = ∠CDF, } \\ { AB = DC, } \end{array} $
∴ $ △ABE ≌ △DCF ( AAS ) $,
∴ $ S _ { △ABE } = S _ { △DCF } $,故 ③ 正确;
∵ $ l _ { 1 } // l _ { 2 } $,$ BA ⊥ l _ { 1 } $,$ DC ⊥ l _ { 2 } $,
∴ 四边形 $ ABCD $ 是矩形,故 ④ 正确.故选 D.
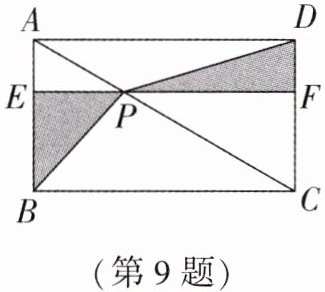
9. (2025·泰州月考)如图,$P$ 是矩形 $ABCD$ 的对角线 $AC$ 上一点,过点 $P$ 作 $EF // BC$,分别交 $AB$,$CD$ 于点 $E$,$F$,连接 $PB$,$PD$。若 $AE = 2$,$PF = 8$,则图中阴影部分的面积为
16
。
]
答案:9. 16 解析:如图,作 $ PM ⊥ AD $ 于点 $ M $,$ PN ⊥ BC $ 于点 $ N $,则四边形 $ AEPM $、四边形 $ DFPM $、四边形 $ CFPN $、四边形 $ BEPN $ 都是矩形,

∴ $ S _ { △ADC } = S _ { △ABC } $,$ S _ { △AMP } = S _ { △AEP } $,$ S _ { △PBE } = S _ { △PBN } $,$ S _ { △PFD } = S _ { △PDM } $,$ S _ { △PFC } = S _ { △PCN } $,
∴ $ S _ { △DFP } = S _ { △PBE } = \frac { 1 } { 2 } × 2 × 8 = 8 $,
∴ $ S _ { 阴影 } = 8 + 8 = 16 $.
10. (2025·绵阳期中)如图,在 $△ ABC$ 中,$AB = 6$,$AC = 8$,$BC = 10$,$P$ 为边 $BC$ 上一动点(且点 $P$ 不与点 $B$,$C$ 重合),$PE ⊥ AB$ 于点 $E$,$PF ⊥ AC$ 于点 $F$,$M$ 为 $EF$ 的中点。设 $AM$ 的长为 $x$,则 $x$ 的取值范围是
$2.4 ≤ x < 4$
。
]
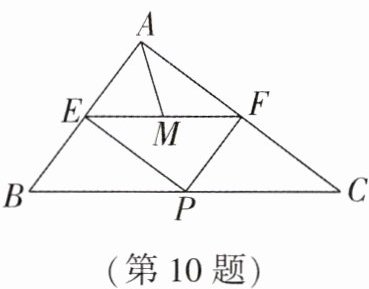
答案:10. $ 2.4 ≤ x < 4 $ 解析:连接 $ AP $.
∵ $ AB = 6 $,$ AC = 8 $,$ BC = 10 $,
∴ $ AB ^ { 2 } + AC ^ { 2 } = 36 + 64 = 100 $.
∵ $ BC ^ { 2 } = 100 $,
∴ $ AB ^ { 2 } + AC ^ { 2 } = BC ^ { 2 } $,
∴ $ ∠BAC = 90° $.
∵ $ PE ⊥ AB $,$ PF ⊥ AC $,
∴ $ ∠AEP = ∠AFP = ∠BAC = 90° $,
∴ 四边形 $ AEPF $ 是矩形,
∴ $ AP = EF $.
∵ $ ∠BAC = 90° $,$ M $ 为 $ EF $ 的中点,
∴ $ AM = \frac { 1 } { 2 } EF = \frac { 1 } { 2 } AP $.
当 $ AP ⊥ BC $ 时,$ AP $ 的值最小.
∵ $ S _ { △BAC } = \frac { 1 } { 2 } × 6 × 8 = \frac { 1 } { 2 } × 10 × AP $,解得 $ AP = 4.8 $,
∴ $ AP ≥ 4.8 $,
∴ $ 2 AM ≥ 4.8 $,
∴ $ AM ≥ 2.4 $(即 $ x ≥ 2.4 $). 当 $ P $ 和 $ C $ 重合时,$ AM = 4 $.
∵ 点 $ P $ 和点 $ B $,$ C $ 不重合,
∴ $ AP < 8 $,
∴ $ x < 4 $,
∴ $ x $ 的取值范围是 $ 2.4 ≤ x < 4 $.
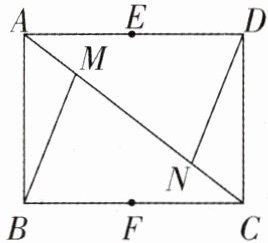
11. (大庆中考)如图,在矩形 $ABCD$ 中,$AB = 3$,$BC = 4$,$M$,$N$ 在对角线 $AC$ 上,且 $AM = CN$,$E$,$F$ 分别是 $AD$,$BC$ 的中点。
(1) 求证:$△ ABM ≌ △ CDN$;
(2) 点 $G$ 是对角线 $AC$ 上的点,$∠ EGF = 90^{\circ}$,求 $AG$ 的长。
]
答案:11. (1)
∵ 四边形 $ ABCD $ 是矩形,
∴ $ AB // CD $,
∴ $ ∠MAB = ∠NCD $.
在 $ △ABM $ 和 $ △CDN $ 中,$ \{ \begin{array} { l } { AB = CD, } \\ { ∠MAB = ∠NCD, } \\ { AM = CN, } \end{array} $
∴ $ △ABM ≌ △CDN ( SAS ) $.
(2) 连接 $ EF $,交 $ AC $ 于点 $ O $.
∵ 四边形 $ ABCD $ 是矩形,
∴ $ AD = BC $,$ ∠ABC = 90° $,
∴ $ AC = \sqrt { AB ^ { 2 } + BC ^ { 2 } } = 5 $.
∵ $ E $,$ F $ 分别是 $ AD $,$ BC $ 的中点,
∴ $ AE = BF = ED = FC $,
∴ 四边形 $ ABFE $ 是矩形,
∴ $ EF = AB = 3 $. 在 $ △AEO $ 和 $ △CFO $ 中,$ \{ \begin{array} { l } { ∠EOA = ∠FOC, } \\ { ∠EAO = ∠FCO, } \\ { AE = CF, } \end{array} $
∴ $ △AEO ≌ △CFO ( AAS ) $,
∴ $ EO = FO $,$ AO = CO = \frac { 5 } { 2 } $,
∴ $ O $ 为 $ EF $,$ AC $ 的中点.
∵ $ ∠EGF = 90° $,
∴ $ OG = \frac { 1 } { 2 } EF = \frac { 3 } { 2 } $,
∴ $ AG = OA - OG = 1 $ 或 $ AG = OA + OG = 4 $,
∴ $ AG $ 的长为 1 或 4.
12. 已知平面上四点 $A(0,0)$,$B(4,0)$,$C(4,2)$,$D(0,2)$,直线 $y = mx - m + 2$ 将四边形 $ABCD$ 分成面积相等的两部分,则 $m$ 的值为
-1
。
答案:12. -1 解析:
∵ 点 $ A ( 0,0 ) $,$ B ( 4,0 ) $,$ C ( 4,2 ) $,$ D ( 0,2 ) $,
∴ 四边形 $ ABCD $ 为矩形.
∵ 直线 $ y = m x - m + 2 $ 将四边形 $ ABCD $ 分成面积相等的两部分,
∴ 直线 $ y = m x - m + 2 $ 过矩形 $ ABCD $ 的对角线的交点. 而矩形 $ ABCD $ 的对角线的交点坐标为 $ ( 2,1 ) $,
∴ $ 2 m - m + 2 = 1 $,
∴ $ m = - 1 $.
13. (2025·淮安模拟)【问题发现】(1)如图①,矩形 $ABCD$ 中,$AB = 9$,$BC = 12$,点 $P$ 是矩形 $ABCD$ 内一点,过点 $P$ 作 $EF ⊥ AD$,分别交 $AD$,$BC$ 于点 $E$,$F$,$PE = 4$,$AE = 3$。则:
① $PC =$
$\sqrt { 106 }$
;
② $PA^2 + PC^2$ 与 $PB^2 + PD^2$ 的关系是
$PA ^ { 2 } + PC ^ { 2 } = PB ^ { 2 } + PD ^ { 2 }$
。
【类比探究】(2)如图②,点 $P$ 是矩形 $ABCD$ 外一点,过点 $P$ 作 $EF ⊥ AD$,分别交 $AD$,$BC$ 反向延长线于点 $E$,$F$,②中结论还成立吗?若成立,请说明理由。
【拓展延伸】(3)如图③,在 $Rt△ ABC$ 中,$∠ BAC = 90^{\circ}$,$P$ 是 $Rt△ ABC$ 外一点,$PA = 2$,$PB = 5$,$PC = 3$,则 $BC$ 的最小值为
$\sqrt { 30 } - 2$
。
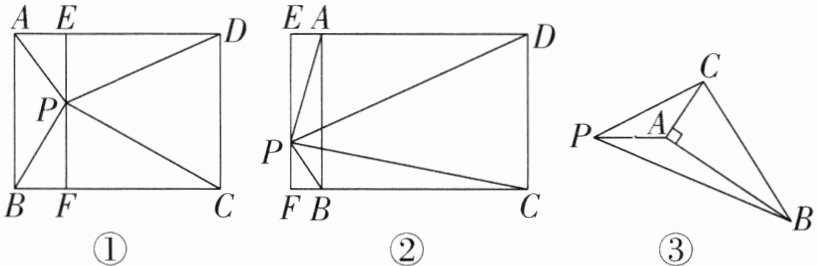
]
答案:13. (1) ① $ \sqrt { 106 } $ 解析:
∵ 四边形 $ ABCD $ 是矩形,$ AB = 9 $,$ BC = 12 $,
∴ $ AD = BC = 12 $,$ ∠BAD = ∠ABC = ∠ADC = ∠BCD = 90° $.
∵ 过点 $ P $ 作 $ EF ⊥ AD $,分别交 $ AD $,$ BC $ 于点 $ E $,$ F $,
∴ $ ∠AEF = ∠DEF = 90° $,
∴ 四边形 $ ABFE $ 和四边形 $ DCFE $ 都是矩形,
∴ $ EF = AB = 9 $,$ BF = AE = 3 $,
∴ $ CF = DE = AD - AE = 12 - 3 = 9 $.
∵ $ PE = 4 $,
∴ $ PA = \sqrt { AE ^ { 2 } + PE ^ { 2 } } = \sqrt { 3 ^ { 2 } + 4 ^ { 2 } } = 5 $,$ PD = \sqrt { DE ^ { 2 } + PE ^ { 2 } } = \sqrt { 9 ^ { 2 } + 4 ^ { 2 } } = \sqrt { 97 } $.
∵ $ PF = EF - PE = 9 - 4 = 5 $,
∴ $ PB = \sqrt { BF ^ { 2 } + PF ^ { 2 } } = \sqrt { 3 ^ { 2 } + 5 ^ { 2 } } = \sqrt { 34 } $,$ PC = \sqrt { CF ^ { 2 } + PF ^ { 2 } } = \sqrt { 9 ^ { 2 } + 5 ^ { 2 } } = \sqrt { 106 } $.
② $ PA ^ { 2 } + PC ^ { 2 } = PB ^ { 2 } + PD ^ { 2 } $ 解析:$ PA ^ { 2 } + PC ^ { 2 } = 5 ^ { 2 } + ( \sqrt { 106 } ) ^ { 2 } = 131 $,$ PB ^ { 2 } + PD ^ { 2 } = ( \sqrt { 34 } ) ^ { 2 } + ( \sqrt { 97 } ) ^ { 2 } = 131 $,
∴ $ PA ^ { 2 } + PC ^ { 2 } = PB ^ { 2 } + PD ^ { 2 } $.
(2) 成立,理由如下:
∵ 四边形 $ ABCD $ 是矩形,
∴ $ ∠BAD = ∠ABC = ∠ADC = ∠BCD = 90° $,
∴ $ ∠EAB = ∠FBA = 90° $.
∵ 过点 $ P $ 作 $ EF ⊥ AD $,分别交 $ AD $,$ BC $ 反向延长线于点 $ E $,$ F $,
∴ $ ∠AEF = 90° $,
∴ 四边形 $ ABFE $ 和四边形 $ DCFE $ 都是矩形,
∴ $ AE = BF $,$ DE = CF $.
∵ $ PD ^ { 2 } = DE ^ { 2 } + PE ^ { 2 } = CF ^ { 2 } + PE ^ { 2 } $,$ PA ^ { 2 } = AE ^ { 2 } + PE ^ { 2 } = BF ^ { 2 } + PE ^ { 2 } $,
∴ $ PD ^ { 2 } - PA ^ { 2 } = CF ^ { 2 } - BF ^ { 2 } $.
∵ $ PC ^ { 2 } = CF ^ { 2 } + PF ^ { 2 } $,$ PB ^ { 2 } = BF ^ { 2 } + PF ^ { 2 } $,
∴ $ PC ^ { 2 } - PB ^ { 2 } = CF ^ { 2 } - BF ^ { 2 } $,
∴ $ PC ^ { 2 } - PB ^ { 2 } = PD ^ { 2 } - PA ^ { 2 } $,
∴ $ PA ^ { 2 } + PC ^ { 2 } = PB ^ { 2 } + PD ^ { 2 } $.
(3) $ \sqrt { 30 } - 2 $ 解析:如图,作 $ PM ⊥ CA $ 交 $ CA $ 的延长线于点 $ M $,则 $ ∠PMC = 90° $,
∴ $ PC ^ { 2 } = PM ^ { 2 } + CM ^ { 2 } $,$ PA ^ { 2 } = PM ^ { 2 } + AM ^ { 2 } $. 作 $ BN ⊥ PM $ 交 $ PM $ 的延长线于点 $ N $,作 $ CT ⊥ NB $ 交 $ NB $ 的延长线于点 $ T $,连接 $ AT $,$ PT $.
∵ $ ∠BAC = 90° $,
∴ $ ∠BAM = 90° $.
∵ $ ∠AMN = ∠N = ∠CTN = 90° $,
∴ 四边形 $ ABNM $ 和四边形 $ CTNM $ 都是矩形,
∴ $ TN = CM $,$ BN = AM $,
∴ $ PT ^ { 2 } = PN ^ { 2 } + TN ^ { 2 } = PN ^ { 2 } + CM ^ { 2 } $,$ PB ^ { 2 } = PN ^ { 2 } + BN ^ { 2 } = PN ^ { 2 } + AM ^ { 2 } $,$ PC ^ { 2 } = PM ^ { 2 } + CM ^ { 2 } $,$ PA ^ { 2 } = PM ^ { 2 } + AM ^ { 2 } $,
∴ $ PT ^ { 2 } - PC ^ { 2 } = PN ^ { 2 } - PM ^ { 2 } $,$ PB ^ { 2 } - PA ^ { 2 } = PN ^ { 2 } - PM ^ { 2 } $