2. 某校组织共青团员开展志愿服务活动,每个志愿者都可以从以下三个项目中任选一项参加:
① 敬老院做义工;② 文化广场地面保洁;③ 路口文明岗值勤.小明和小慧选择参加同一项目的概率是(
A
).
A.$\frac{1}{3}$
B.$\frac{2}{3}$
C.$\frac{1}{9}$
D.$\frac{2}{9}$
答案:A
3. 甲、乙、丙 3 人用牌面分别为 A、2、3 的 3 张扑克牌做游戏(牌的背面完全相同),将 3 张牌打乱顺序正面朝下放置,然后由甲、乙、丙 3 人依次从中抽出 1 张(不放回),且规定抽到 A 者获胜,下面对甲、乙、丙 3 人获胜概率的表述正确的是(
D
).
A.甲先抽,甲获胜的概率最大
B.乙获胜的概率比甲小,比丙大
C.丙最后抽,丙获胜的概率最小
D.3 人获胜的概率相同,与抽牌的顺序无关
答案:D
4. 在某校组织的一次物理、化学实验操作考试中,规定每位考生在 3 个物理实验(用纸签 A、B、C 表示)和 3 个化学实验(用纸签 D、E、F 表示)中各抽取 1 个实验进行考试.
(1) 用列表法或树状图法列出所有可能出现的结果;
(2) 该校某考生考试时抽到物理实验 B 和化学实验 F(记作事件 M)的概率是多少?
答案:解: (1)列表如下:
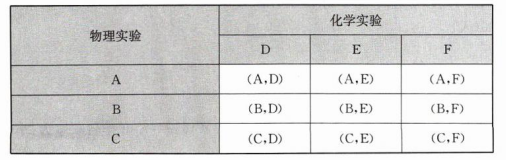
(2)从表格可以看出,所有可能出现的结果共有9种,并且它们是等可能的,其中事件M出现了一次,
∴$P(\mathrm {M})=\frac {1}{9}$
答:小刚考试时抽到物理实验和化学实验的概率是$\frac {1}{9}$
1. 用抽签的办法从 3 名同学中选 2 名去看电影,这种办法公平吗?如果是你,你愿意先抽还是后抽?为什么?
答案:解:公平,先抽和后抽都一样,因为每人中签的概率都为$\frac {2}{3}。$
2. 甲、乙两人做游戏.规则如下:在一只不透明的袋中装有分别标有数字 1,2,3,4 的四个小球(除标号外,其余都相同),甲从袋中任意摸出 1 个小球,小球上的数字记为 a.在另一只不透明的袋中装有分别标有数字 1,2 的两张卡片(除标号外,其余都相同),乙从袋中任意摸出 1 张卡片,卡片上的数字记为 b.然后计算这两个数的和,即 a + b.若 a + b 为奇数,则甲获胜;否则,乙获胜.
(1) 用列表法或树状图法,求 a + b 所有可能出现的结果总数.
(2) 这个游戏公平吗?如果公平,请说明理由;如果不公平,谁获胜的概率更大?
答案:解: (1)列表如下
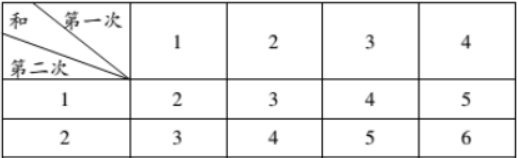
一共有8种等可能的结果
(2)∵P(甲胜$)=\frac {4}{8}=\frac {1}{2},$P(乙胜$)=\frac {4}8=\frac {1}{2}$
∴这个游戏对双方公平