4. (苏州)额定电压均为$6\ V$的甲、乙两灯,其$I-U$图线如图所示。下列说法中正确的是 (
D
)

A.甲、乙两灯的电阻均随电压的增大而减小
B.甲、乙两灯的额定功率之比为$4:1$
C.甲、乙两灯并联接在电压为$2\ V$的电源两端时,电阻之比为$3:2$
D.甲、乙两灯串联接在电压为$8\ V$的电源两端时,实际功率之比为$1:3$
答案:4.D
解析:
解:
A. 由I-U图线可知,甲、乙两灯的电流随电压增大而增大,且图线斜率减小,根据$R=\frac{U}{I}$,电阻随电压增大而增大,A错误。
B. 额定电压6V时,$I_{甲}=0.6A$,$I_{乙}=0.3A$,$P_{甲}=U I_{甲}=6V×0.6A=3.6W$,$P_{乙}=U I_{乙}=6V×0.3A=1.8W$,$P_{甲}:P_{乙}=2:1$,B错误。
C. 并联2V时,$I_{甲}=0.3A$,$I_{乙}=0.2A$,$R_{甲}=\frac{2V}{0.3A}=\frac{20}{3}Ω$,$R_{乙}=\frac{2V}{0.2A}=10Ω$,$R_{甲}:R_{乙}=2:3$,C错误。
D. 串联接8V电源,电流相等,设电流为I,$U_{甲}+U_{乙}=8V$。由图知,当$I=0.3A$时,$U_{甲}=2V$,$U_{乙}=6V$,满足$2V+6V=8V$。$P_{甲}=U_{甲}I=2V×0.3A=0.6W$,$P_{乙}=U_{乙}I=6V×0.3A=1.8W$,$P_{甲}:P_{乙}=1:3$,D正确。
答案:D
5. (扬州)如图所示,电源电压保持不变,开关$S$闭合后,调节滑动变阻器的滑片,下列说法中正确的是 (
B
)

A.滑片向左移动,电流表示数增大,电压表示数减小
B.滑片向左移动,电流表、电压表示数都增大
C.滑片向右移动,电流表、电压表示数都增大
D.滑片向右移动,电流表示数减小,电压表示数增大
答案:5.B
解析:
解:由电路图可知,灯泡L与滑动变阻器串联,电压表测灯泡L两端的电压,电流表测电路中的电流。
滑片向左移动时,滑动变阻器接入电路的电阻减小,电路总电阻减小。根据$I = \frac{U}{R}$,电源电压U不变,电路中电流I增大,即电流表示数增大。由$U_L = IR_L$,灯泡电阻$R_L$不变,电流I增大,灯泡两端电压$U_L$增大,即电压表示数增大,故A错误,B正确。
滑片向右移动时,滑动变阻器接入电路的电阻增大,电路总电阻增大。根据$I = \frac{U}{R}$,电路中电流I减小,电流表示数减小。由$U_L = IR_L$,灯泡两端电压$U_L$减小,电压表示数减小,故C、D错误。
结论:B
6. (南京)如图所示,电源电压恒为$4.5\ V$,定值电阻$R_0$的阻值为$10\ \Omega$,滑动变阻器的最大阻值为$30\ \Omega$,电阻箱$R_x$最大阻值为$999.9\ \Omega$,电流表量程为$0\sim0.6\ A$,电压表量程为$0\sim3\ V$。闭合开关$S$,下列说法中正确的是 (
D
)
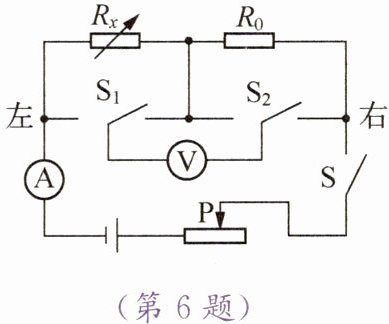
A.$S_1$、$S_2$均向左闭合,$R_x$允许接入电路的最大阻值为$20\ \Omega$
B.$S_1$、$S_2$均向右闭合,电路允许消耗的最大功率为$2.7\ W$
C.$S_1$向左闭合、$S_2$向右闭合,$R_x$允许接入电路的最大阻值为$60\ \Omega$
D.$S_1$向右闭合、$S_2$向左闭合,调节$R_x$使电流表示数减半后,其阻值一定大于原来的$2$倍
答案:6.D
7. (南京)南京长江大桥是我市的地标性建筑,现已焕然一新并顺利通车,如图(a)所示。图(b)中,大桥上玉兰花灯内的钠灯全部换为$LED$灯后,总功率减少了约$180\ kW$。与原来相比,所有灯工作$5\ h$可节约电能
900
$ kW· h$。

答案:7.900
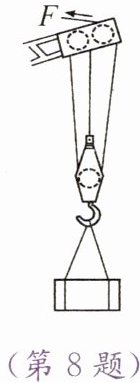
8. (南京)建筑工地上,起重机吊臂上的滑轮组如图所示。在匀速起吊重$4.2×10^3\ N$的物体时,物体$5\ s$内上升了$6\ m$,此过程中有用功为
$2.52×10^4$
$ J$,钢丝绳移动的速度为
3.6
$ m/s$;若滑轮组的机械效率为$70\%$,则额外功为
$1.08×10^4$
$ J$,拉力$F$为
$2×10^3$
$ N$,其功率为
$7.2×10^3$
$ W$。
答案:8.$2.52×10^4$ 3.6 $1.08×10^4$ $2×10^3$ $7.2×10^3$
解析:
有用功:$W_{有}=Gh=4.2×10^{3}\ N×6\ m=2.52×10^{4}\ J$
物体上升速度:$v_{物}=\frac{h}{t}=\frac{6\ m}{5\ s}=1.2\ m/s$,由图知$n=3$,钢丝绳移动速度:$v=nv_{物}=3×1.2\ m/s=3.6\ m/s$
由$\eta=\frac{W_{有}}{W_{总}}$得总功:$W_{总}=\frac{W_{有}}{\eta}=\frac{2.52×10^{4}\ J}{70\%}=3.6×10^{4}\ J$,额外功:$W_{额}=W_{总}-W_{有}=3.6×10^{4}\ J-2.52×10^{4}\ J=1.08×10^{4}\ J$
钢丝绳移动距离:$s=nh=3×6\ m=18\ m$,由$W_{总}=Fs$得拉力:$F=\frac{W_{总}}{s}=\frac{3.6×10^{4}\ J}{18\ m}=2×10^{3}\ N$
拉力功率:$P=Fv=2×10^{3}\ N×3.6\ m/s=7.2×10^{3}\ W$
$2.52×10^{4}$;$3.6$;$1.08×10^{4}$;$2×10^{3}$;$7.2×10^{3}$