1. 用图象法解二元一次方程组$\left\{\begin{array}{l} x+2y= 4,\\ 2x-y= 3.\end{array} \right. $
答案:解:如答图,在同一直角坐标系中画出直线$y=2x-3$,$y=-\dfrac{1}{2}x+2$,可得两条直线的交点坐标是$(2,1)$.
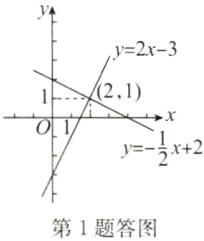
∴二元一次方程组$\begin{cases}x + 2y = 4\\2x - y = 3\end{cases}$的解为$\begin{cases}x = 2\\y = 1\end{cases}$.
2. 在同一平面直角坐标系内,一次函数$y= 2x+3与y= 2x-3$的图象有什么样的位置关系?你能从中知道方程组$\left\{\begin{array}{l} 2x-y+3= 0,\\ 2x-y-3= 0\end{array} \right. $的解的情况吗?
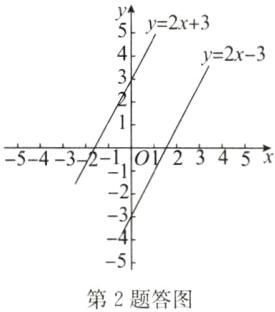
答案:解:一次函数$y=2x+3$与$y=2x-3$的图象如答图所示.由图象可知两条直线平行,
故方程组$\begin{cases}2x - y + 3 = 0\\2x - y - 3 = 0\end{cases}$无解.
3. 正比例函数$y= -3x的图象与一次函数y= kx+b的图象交于点P(m,3)$,一次函数的图象经过点$B(1,1)$,与$y轴的交点为D$,与$x轴的交点为C$.
(1)求一次函数的表达式;
(2)求点$D$的坐标;
(3)求$\triangle COP$的面积;
(4)不解关于$x$,$y的方程组\left\{\begin{array}{l} y= -3x,\\ y= kx+b,\end{array} \right. $直接写出方程组的解.
答案:
(1)
∵正比例函数$y=-3x$的图象与一次函数$y=kx+b$的图象交于点$P(m,3)$,
∴$-3m=3$,解得$m=-1$,
∴$P(-1,3)$.
把$(1,1)$和$(-1,3)$分别代入一次函数$y=kx+b$,
得$\begin{cases}k + b = 1\\-k + b = 3\end{cases}$,解得$\begin{cases}b = 2\\k = -1\end{cases}$,
∴一次函数的表达式是$y=-x+2$.
(2)由
(1)知一次函数的表达式是$y=-x+2$,
令$x=0$,则$y=2$,即点$D(0,2)$.
(3)由
(1)知一次函数的表达式是$y=-x+2$,
令$y=0$,得$-x+2=0$,解得$x=2$,
∴点$C(2,0)$,
∴$OC=2$,
∵$P(-1,3)$,
∴$\triangle COP$的面积$=\dfrac{1}{2}OC\cdot |y_{P}|=\dfrac{1}{2}× 2× 3=3$.
(4)
∵正比例函数$y=-3x$的图象与一次函数$y=kx+b$的图象交于点$P(-1,3)$,
∴方程组的解为$\begin{cases}x = -1\\y = 3\end{cases}$.