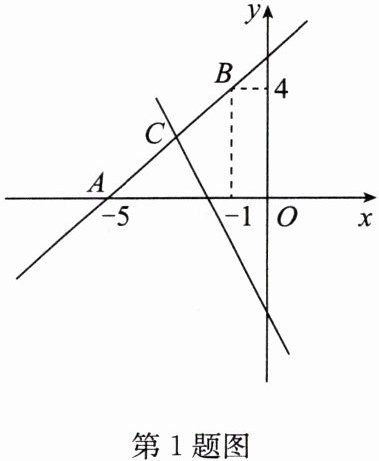
1. 如图,直线 $ y = kx + b $ 经过点 $ A(-5,0) $,$ B(-1,4) $。
(1) 求直线 $ AB $ 的函数表达式;
(2) 若直线 $ y = -2x - 4 $ 与直线 $ AB $ 相交于点 $ C $,求点 $ C $ 的坐标;
(3) 根据图象,直接写出关于 $ x $ 的不等式 $ kx + b > -2x - 4 $ 的解集。
答案:1.解:
(1)
∵直线y=kx+b经过点A(-5,0),B(-1,4),
∴{-5k+b=0,-k+b=4,
∴{k=1,b=5.
∴直线AB的函数表达式为y=x+5.
(2)
∵直线y=-2x-4与直线AB相交于点C,
∴{y=x+5,y=-2x-4,
∴{x=-3,y=2,
∴C(-3,2).
(3)x>-3.
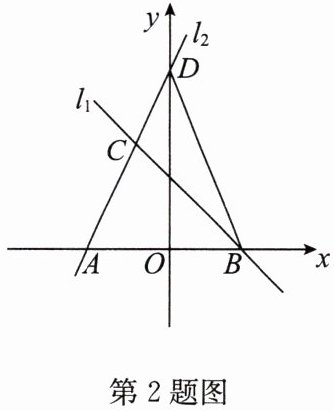
2. 如图,直线 $ l_1 $ 的函数表达式为 $ y = -x + 2 $,直线 $ l_1 $ 与 $ x $ 轴交于点 $ B $,直线 $ l_2 $ 经过点 $ D(0,5) $,与直线 $ l_1 $ 交于点 $ C(-1,m) $,且与 $ x $ 轴交于点 $ A $。
(1) 求点 $ C $ 的坐标及直线 $ l_2 $ 的函数表达式;
(2) 连接 $ BD $,求 $ \triangle BCD $ 的面积。
答案:2.解:
(1)
∵直线l₁经过点C(-1,m),
∴m=1+2=3,
∴C(-1,3).
设直线l₂的函数表达式为y=kx+b,
将(0,5),(-1,3)代入上式得,
∴{b=5,-k+b=3,解得{k=2,b=5,
∴直线l₂的函数表达式为y=2x+5.
(2)将x=0代入直线l₁的函数表达式,得y=2,
∴直线BC与y轴的交点坐标为(0,2).
将y=0代入直线l₁的函数表达式得,-x+2=0,解得
x=2,则B(2,0),
∴△BCD的面积为$\frac{1}{2}$×(5-2)×[2-(-1)]=$\frac{9}{2}$.