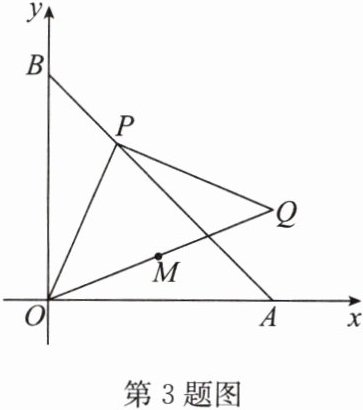
3. 如图,$ A(4, 0) $,$ B(0, 4) $,点 $ P $ 在线段 $ AB $ 上运动,$ PQ \perp PO $ 且 $ PQ = PO $.
(1) 试说明点 $ Q $ 在某一确定的直线上;
(2) $ M $ 是线段 $ OQ $ 的中点,当点 $ P $ 从点 $ A $ 运动到点 $ B $ 时,求点 $ M $ 运动的路径长.
答案:解:
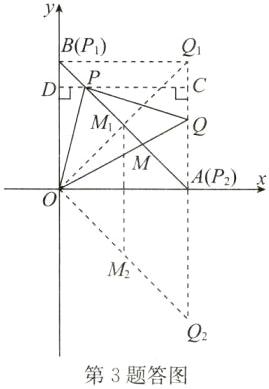
(1)如答图,过点P作CD⊥y轴于点D,过点Q作QC⊥CD于点C,则点Q的横坐标为线段CD的长. 设PD=m,DO=n,则P(m,n).
∵A(4,0),B(0,4),
∴设直线AB的函数表达式为y=kx+4, 则4k+4=0,解得k= - 1,
∴直线AB的函数表达式为y= - x+4,
∴n= - m+4,
∴m+n=4.
∵PD⊥OD,PC⊥CQ,OP⊥PQ,
∴∠ODP=∠PCQ=∠OPQ=90°,
∴∠DOP+∠DPO=∠DPO+∠CPQ=90°,
∴∠DOP=∠CPQ. 又
∵PQ=PO,
∴△ODP≌△PCQ(AAS),
∴PC=DO.
∵CD=CP+PD,
∴CD=OD+PD=m+n=4.
∴点Q的横坐标为4,
∴当点P在线段AB上运动时,点Q的横坐标始终为4.
∴点Q在确定的直线x=4上.
(2)由
(1)知,当点P(m,n)在线段AB上运动时,点Q的横坐标为4,由题意知M是线段OQ的中点,设M(a,b),则a=$\frac{0 + 4}{2}$=2,
∴点M在直线x=2上.当点P运动到与点A重合时,由答图可知,点Q与点Q₂(4, - 4)重合,此时a=2,b=$\frac{0 - 4}{2}$= - 2,
∴点M会与点M₂(2, - 2)重合.同理,当点P运动到与点B重合时,点M会与点M₁(2,2)重合.
∴当点P从点A运动到点B时,点M运动的路径长就是线段M₁M₂的长.
∵M₁M₂=2 - ( - 2)=4,
∴点P从点A运动到点B时,点M运动的路径长为4.