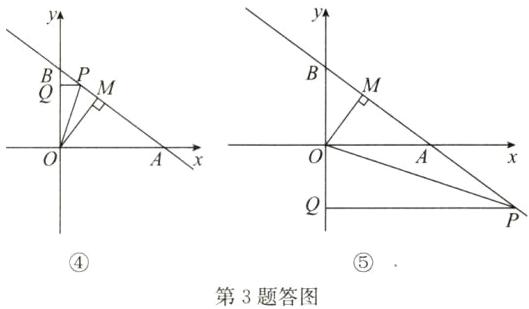
3. 如图, 直线 $ l: y = kx + 3 $ 与 $ x $ 轴、 $ y $ 轴分别交于 $ A $, $ B $ 两点, $ \frac{OB}{OA} = \frac{3}{4} $, $ OM \perp AB $, 垂足为 $ M $, 点 $ P $ 为直线 $ l $ 上的一个动点 (不与点 $ A $, $ B $ 重合).
(1) 求直线 $ l $ 的函数表达式.
(2) 当点 $ P $ 运动到什么位置时, $ \triangle BOP $ 的面积是 $ 6 $?
(3) 在 $ y $ 轴上是否存在点 $ Q $, 使得以 $ O $, $ P $, $ Q $ 为顶点的三角形与 $ \triangle OMP $ 全等? 若存在, 请求出所有符合条件的点 $ P $ 的坐标; 若不存在, 请说明理由.
答案:3.解:
(1)
∵直线l:y=kx+3与y轴交于点B,
∴B(0,3),即OB=3.
∵$\frac{OB}{OA}=\frac{3}{4}$,
∴OA=4,即A(4,0).
∵点A在直线l上,
∴4k+3=0,解得k=-$\frac{3}{4}$.
∴直线l的函数表达式为y=-$\frac{3}{4}$x+3.
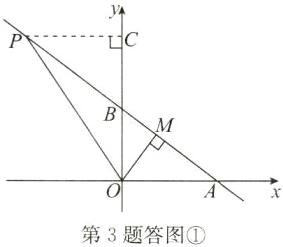
(2)如答图①,过点P作PC⊥y轴于点C,
∴S△BOP=$\frac{1}{2}$OB·PC=6,
∴PC=4.
∴点P的横坐标为4或-4.又
∵点P是直线l上的一个动点且不与点A,B重合,
∴点P的横坐标为-4,
∴点P的纵坐标为-$\frac{3}{4}$×(-4)+3=6.
∴当点P的坐标为(-4,6)时,△BOP的面积是6.
(3)存在满足条件的点P,Q.
∵OM⊥AB,AB=$\sqrt{OA^2+OB^2}=\sqrt{4^2+3^2}=5$,
∴∠OMP=90°,
∴OM=$\frac{OA·OB}{AB}=\frac{12}{5}$.
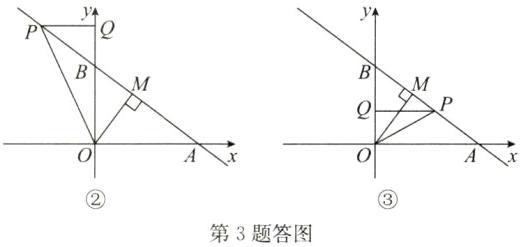
∴以O,P,Q为顶点的三角形与△OMP全等时,∠OQP=90°.分两种情况讨论:①若△OMP≌△PQO 则PQ=OM=$\frac{12}{5}$,即点P的横坐标为-$\frac{12}{5}$或$\frac{12}{5}$,如答图②和答图③,此时点P的纵坐标为-$\frac{3}{4}$×(-$\frac{12}{5}$)+3=$\frac{24}{5}$或-$\frac{3}{4}$×$\frac{12}{5}$+3=$\frac{6}{5}$,
∴点P的坐标为(-$\frac{12}{5}$,$\frac{24}{5}$)或($\frac{12}{5}$,$\frac{6}{5}$);
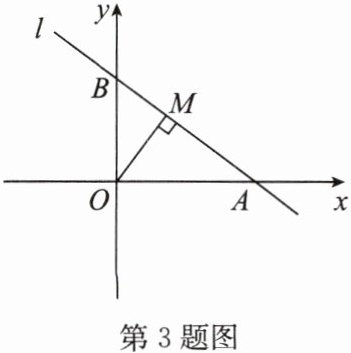
②若△OMP≌△OQP,则OQ=OM=$\frac{12}{5}$,即点P,Q的纵坐标均为-$\frac{12}{5}$或$\frac{12}{5}$,如答图④和答图⑤,由-$\frac{3}{4}$x+3=-$\frac{12}{5}$,解得x=$\frac{36}{5}$;由-$\frac{3}{4}$x+3=$\frac{12}{5}$,解得x=$\frac{4}{5}$,
∴点P的坐标为($\frac{36}{5}$,-$\frac{12}{5}$)或($\frac{4}{5}$,$\frac{12}{5}$).综上,符合条件的点P的坐标为(-$\frac{12}{5}$,$\frac{24}{5}$)或($\frac{12}{5}$,$\frac{6}{5}$)或($\frac{36}{5}$,-$\frac{12}{5}$)或($\frac{4}{5}$,$\frac{12}{5}$).