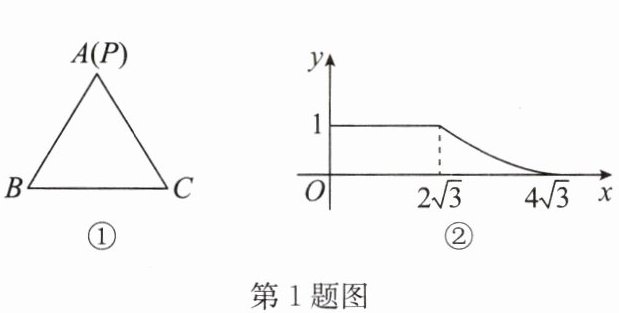
1. 如图①,点 $P$ 从等边三角形 $ABC$ 的顶点 $A$ 出发,沿直线运动到三角形内部一点,再从该点沿直线运动到顶点 $B$。设点 $P$ 运动的路程为 $x$,$\frac{PB}{PC}= y$,图②是点 $P$ 运动时 $y$ 随 $x$ 变化的关系图象,则等边三角形 $ABC$ 的边长为( )
A.$6$
B.$3$
C.$4\sqrt{3}$
D.$2\sqrt{3}$
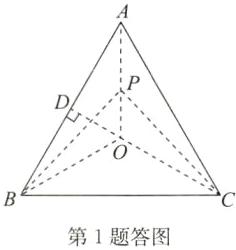
答案:1. A 点拨:如答图,令点P从顶点A出发,沿直线运动到三角形内部一点O,再从点O沿直线运动到顶点B。
结合题图可知,当点P在AO上运动时,$\frac{PB}{PC}=1$,
$\therefore PB=PC$,$AO=2\sqrt{3}$。
又$\because \triangle ABC$为等边三角形,$\therefore \angle BAC = 60^{\circ}$,$AB = AC$。
又$\because AP = AP$,$\therefore \triangle APB\cong \triangle APC(SSS)$,
$\therefore \angle BAO = \angle CAO = 30^{\circ}$。
当点P在OB上运动时,可知点P到达点B时,点P运动的路程为$4\sqrt{3}$,
$\therefore OB = 4\sqrt{3}-2\sqrt{3}=2\sqrt{3}$,即$AO = OB = 2\sqrt{3}$,
$\therefore \angle BAO = \angle ABO = 30^{\circ}$。
如答图,过点O作$OD\perp AB$,垂足为D,
$\therefore AD = BD$,则由勾股定理得$AD = 3$,
$\therefore AB = AD + BD = 6$,
即等边三角形ABC的边长为6。故选A。