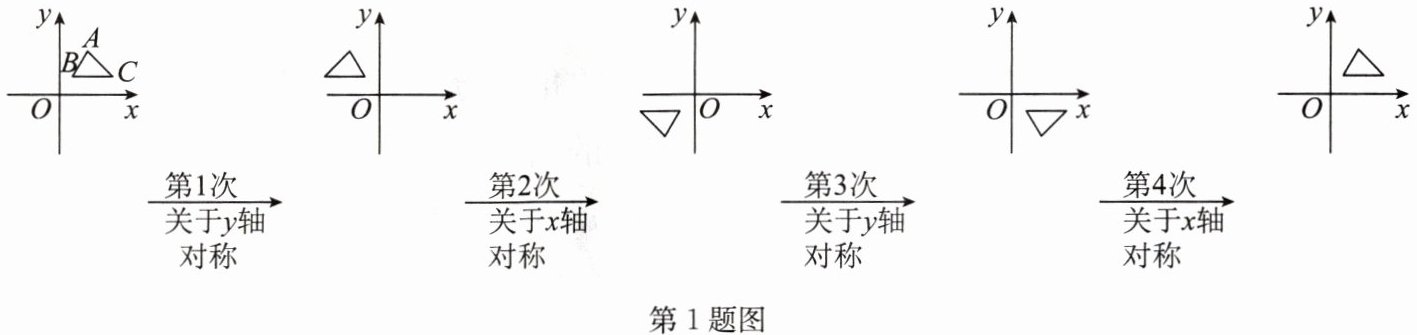
1. 如图, 在平面直角坐标系中, 对$\triangle ABC$进行循环往复的轴对称变换. 若原来点$A的坐标是(1,2)$, 则经过第 2023 次变换后, 点$A$的对应点的坐标为(
A
)
A.$(1,-2)$
B.$(-1,-2)$
C.$(-1,2)$
D.$(1,2)$
答案:A 点拨:点A第1次关于y轴对称后在第二象限,点A 第2次关于x轴对称后在第三象限,点A第3次关于y轴对称后在第四象限,点A第4次关于x轴对称后在第一象限,即点A回到原始位置,所以,每4次变换为一个循环.因为2023÷4=505……3,所以经过第2023次变换后点A的对应点与第3次变换后点A的对应点的位置相同,在第四象限,坐标为(1,−2).故选A.
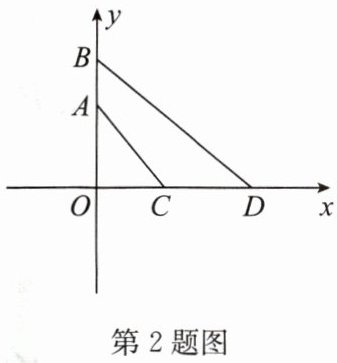
2. 如图, 在平面直角坐标系中, 长为 2 的线段$CD$ (点$D在点C$的右侧) 在$x$轴上移动,$A(0,2),B(0,3)$, 连接$AC,BD$, 则$AC+BD$的最小值为______.
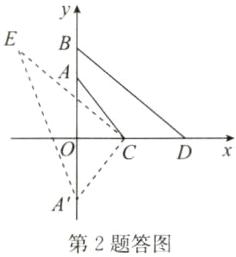
答案:$\sqrt{29}$ 点拨:如答图,将线段DB向左平移到CE的位置,作点A关于原点的对称点A',连接CA',EA',则E(−2,3),A'(0,−2),AC+BD=CA'+CE≥EA',EA'=$\sqrt{5^{2}+2^{2}}=\sqrt{29}$.
∴AC+BD的最小值为 $\sqrt{29}$.
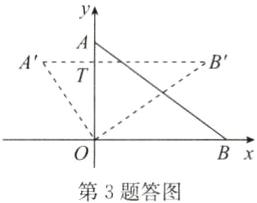
3. 在平面直角坐标系$xOy$中, 点$A(0,3),B(4,0)$, 把$\triangle AOB绕点O$旋转, 使点$A,B分别落在点A',B'$处, 若$A'B'// x$轴, 点$B'$在第一象限, 求点$A的对应点A'$的坐标.
答案:解:如答图,设A'B'交y轴于点T.
∵A(0,3),B(4,0),
∴OA=3,OB=4.
∵∠A'OB'=90°,OT⊥A'B',
OA=OA'=3,OB=OB'=4,
∴AB=A'B'=$\sqrt{OA^{2}+OB^{2}}=\sqrt{3^{2}+4^{2}}=5$,
$\frac{1}{2}OA'\cdot OB'=\frac{1}{2}A'B'\cdot OT$,
∴$OT=\frac{12}{5}$,
∴$A'T=\sqrt{OA'^{2}-OT^{2}}=\sqrt{3^{2}-(\frac{12}{5})^{2}}=\frac{9}{5}$,
∴点A'的坐标为$(-\frac{9}{5},\frac{12}{5})$.