2025年启东中学作业本八年级数学上册苏科版宿迁专版第24页解析答案

1. 如图,在平面直角坐标系中,AD 是 $ Rt\triangle OAB $ 的角平分线,已知点 D 的坐标是 $(0,-4)$,AB 的长是 14,则 $\triangle ABD$ 的面积为

答案：28 点拨: 如答图,过点 D 作 DE⊥AB 于点 E.
由题意可知 OD=4,
∵AD 平分∠OAB,DE⊥AB,DO⊥AO,
∴DE=DO=4. 又
∵AB 的长是 14,
∴$S_{△ABD}=1/2AB·DE=1/2×14×4=28.$

2. 如图,在平面直角坐标系中,已知 $ A(a,0) $,$ B(b,0) $,其中 $ a,b $ 满足 $ |a + 1| + (b - 3)^2 = 0 $.
(1) 填空：$ a = $______,$ b = $______；
(2) 如果在第三象限内有一点 $ M(-2,m) $,请用含 $ m $ 的式子表示 $\triangle ABM$ 的面积；
(3) 在 (2) 的条件下,当 $ m = -\frac{3}{2} $ 时,在 $ y $ 轴上有一点 $ P $,使得 $\triangle BMP$ 的面积与 $\triangle ABM$ 的面积相等,请求出点 $ P $ 的坐标.

答案：

(1)-1 3
(2)解: 如答图①,过点 M 作 MN⊥x 轴于点 N.

∵A(-1,0),B(3,0),
∴AB=3-(-1)=4.
∵M(-2,m)且点 M 在第三象限,
∴MN=|m|=-m.
∴$S_{△ABM}=1/2AB·MN=1/2×4×(-m)=-2m.$
(3)解: 当 m=-3/2 时,M(-2,-3/2),
从而$ S_{△ABM}=1/2×4×$|-3/2|=3.
分两种情况:
若点 P 在 y 轴正半轴上,设点 P(0,k),如答图②,
$S_{△BMP}=5×(3/2 + k)-1/2×2×(3/2 + k)-1/2×5×3/2 - 1/2×3×k=5/2k + 9/4.$
∵△BMP 的面积与△ABM 的面积相等,
∴5/2k + 9/4 = 3,
∴k = 0.3,
∴P(0,0.3).

若点 P 在 y 轴负半轴上且在 MB 的下方时,如答图③,设点 P(0,n),
$S_{△BMP}=-5n - 1/2×2×(-n - 3/2)-1/2×5×3/2 - 1/2×3×(-n)=-5/2n - 9/4.$
∵△BMP 的面积与△ABM 的面积相等,
∴-5/2n - 9/4 = 3,
∴n = -2.1,
∴P(0,-2.1).
综上,点 P 的坐标为(0,0.3)或(0,-2.1).

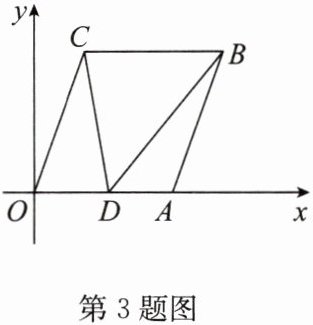
3. 如图,在平面直角坐标系 $ xOy $ 中,已知 $ A(6,0) $,$ B(8,6) $,将线段 $ OA $ 平移至 $ CB $,点 $ D $ 在 $ x $ 轴正半轴上(不与点 $ A $ 重合),连接 $ OC $,$ AB $,$ CD $,$ BD $.
(1) 求点 $ C $ 的坐标；
(2) 当 $\triangle ODC$ 的面积是 $\triangle ABD$ 的面积的 3 倍时,求点 $ D $ 的坐标；
(3) 设 $ \angle OCD = \alpha $,$ \angle DBA = \beta $,$ \angle BDC = \theta $,探究 $ \alpha,\beta,\theta $ 之间的数量关系,并说明理由.

答案：

(1)解: 如答图①,过点 C 作 CF⊥y 轴,过点 B 作 BE⊥x 轴,垂足分别为 F,E.

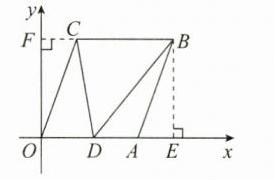
∵A(6,0),B(8,6),OA=CB,
∴FC=AE=8 - 6 = 2,OF=BE=6,
∴C(2,6).
(2)解: 设 D(x,0),当△ODC 的面积是△ABD 的面积的 3 倍时,若点 D 在线段 OA 上,
则 OD=3AD,
∴x + 1/3x = 6,
∴x = 9/2,
∴D(9/2,0).
若点 D 在线段 OA 的延长线上,
则 OD=3AD,
∴x - 1/3x = 6,
∴x = 9,
∴D(9,0).
综上,点 D 的坐标为(9/2,0)或(9,0).
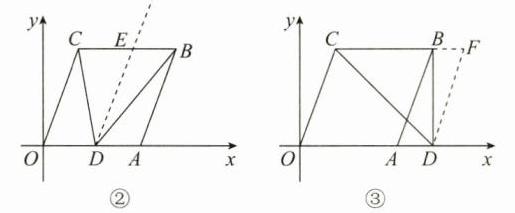
(3)α+β=θ 或 α - β=θ. 理由: 若点 D 在线段 OA 上,如答图②,过点 D 作 DE//OC,交 BC 于点 E.
由平移的性质知 OC//AB,从而 OC//AB//DE,
∴∠OCD=∠CDE,∠EDB=∠DBA.
∴∠CDB=∠CDE+∠EDB=∠OCD+∠DBA,即 α + β=θ.
若点 D 在线段 OA 的延长线上,过点 D 作 DF//AB,与 CB 的延长线交于点 F,如答图③.
由平移可知 OC//AB,
∴DF//OC.
∴∠CDF=∠OCD,∠BDF=∠DBA,
∴∠CDB=∠CDF - ∠BDF=∠OCD - ∠DBA,
∴α - β=θ.
综上,α,β,θ 之间的数量关系为 α + β=θ 或 α - β=θ.