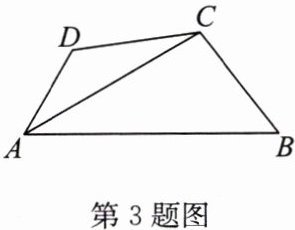
3. 如图,在四边形$ABCD$中,$CB = CD$,$\angle B与\angle D$互补,$\angle BCD = 120^{\circ}$。
求证:$AB + AD = \sqrt{3}AC$。
答案:证明:如答图,延长 AB 至点 E,使$BE = AD$,连接 CE.
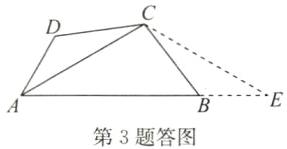
∵$\angle ABC$与$\angle D$互补,
∴$\angle CBE = 180^{\circ} - \angle ABC = \angle D$.
又
∵$CB = CD$,$BE = DA$,
∴$\triangle ADC \cong \triangle EBC(SAS)$.
∴$CA = CE$,$\angle ACD = \angle BCE$.
∴$\angle ACE = \angle ACB + \angle BCE = \angle ACB + \angle ACD = \angle BCD = 120^{\circ}$.
又
∵$CA = CE$,
∴$\angle CAE = \angle E = 30^{\circ}$.
∴$AE = \sqrt{3}AC$.$\therefore AB + AD = \sqrt{3}AC$.