1. 已知一个正数的两个平方根分别是 $2a - 5$ 和 $2a + 1$,另一个实数 $b$ 的立方根是 $2$,$c$ 是 $\sqrt{15}$ 的整数部分.
(1)求 $a,b,c$ 的值;
(2)求 $2a + 4b - c^{2}$ 的平方根.
答案:1.解:
(1)由题意知,2a-5+2a+1=0,b=2³,
∴a=1,b=8.
∵9<15<16,
∴3<√15<4,
∴√15的整数部分为3.
∴c=3.
综上,a=1,b=8,c=3.
(2)
∵a=1,b=8,c=3,
∴2a+4b-c²=2×1+4×8-3²=2+32-9=25.
∵25的平方根为±5,
∴2a+4b-c²的平方根为±5.
2. 已知 $a= \frac{1}{7-\sqrt{47}}$,$b$ 为 $a$ 的小数部分的相反数,求代数式 $a^{3}+b^{3}+18ab$ 的值.
答案:2.解:a=1/(7-√47)=(7+√47)/2,
∵6<√47<7,
∴6<a<7.
∴a的小数部分为a-6.
∵b为a的小数部分的相反数,
∴b=6-a.
∴a+b=6.
∴a³+b³+18ab=(a+b)³-3ab(a+b)+18ab=6³-18ab+18ab=216.
3. 大家知道 $\sqrt{2}$ 是无理数,而无理数是无限不循环小数,因此 $\sqrt{2}$ 的小数部分我们不可能全部写出来. 将这个数减去其整数部分,差就是小数部分,因为 $\sqrt{2}$ 的整数部分是 $1$,于是用 $\sqrt{2}-1$ 来表示 $\sqrt{2}$ 的小数部分. 又例如: $\because \sqrt{4}<\sqrt{7}<\sqrt{9}$,即 $2<\sqrt{7}<3$,$\therefore \sqrt{7}$ 的整数部分是 $2$,小数部分是 $\sqrt{7}-2$.
(1) $\sqrt{17}$ 的整数部分是
4
,小数部分是
$\sqrt{17}-4$
;
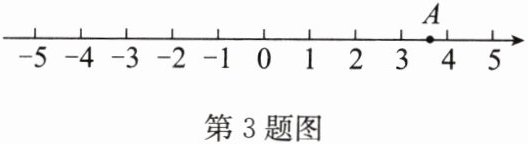
(2)点 $A$ 表示的数为无理数,在数轴上的位置如图所示,若其整数部分为 $m$,小数部分为 $n$,则下列对于 $m,n$ 的说法正确的是
②④
;(填序号)
①$m,n$ 均为有理数;②$1<\sqrt{m}<2$;③$3<m - n<4$;④$3<m + n<4$.
(3)若 $m,n$ 分别是 $6-\sqrt{5}$ 的整数部分和小数部分,求 $3m - n^{2}$ 的值;
解:
∵2<√5<3,
∴3<6-√5<4.
∴m=3,n=6-√5-3=3-√5.
∴3m-n²=3×3-(3-√5)²=9-(9-6√5+5)=6√5-5.
(4)已知 $3 - 2\sqrt{7}$ 的整数部分是 $a$,小数部分是 $b$,试求 $a^{2}+b^{2}$ 的值.
解:
∵2.5<√7<3,
∴-3<3-2√7<-2,
∴a=-3,b=3-2√7-(-3)=6-2√7.
∴a²+b²=(-3)²+(6-2√7)²=9+36-24√7+28=73-24√7.
答案:3.
(1)4 √17-4
(2)②④
(3)解:
∵2<√5<3,
∴3<6-√5<4.
∴m=3,n=6-√5-3=3-√5.
∴3m-n²=3×3-(3-√5)²=9-(9-6√5+5)=6√5-5.
(4)解:
∵2.5<√7<3,
∴-3<3-2√7<-2,
∴a=-3,b=3-2√7-(-3)=6-2√7.
∴a²+b²=(-3)²+(6-2√7)²=9+36-24√7+28=73-24√7.