2025年启东中学作业本八年级数学上册苏科版宿迁专版第20页解析答案

1. 如图,在$\triangle ABC$中,$AB = 6$,$AC = 10$,$AD$是中线,且$AD\perp AB$,则$\triangle ABC$的面积为( )

A.30
B.48
C.24
D.18

答案：
1.C　点拨:如答图,延长AD至点E,使DE=AD,连接CE.
∵AD是中线,
∴BD=CD.又
∵∠ADB=∠EDC,
∴△ABD≌△ECD(SAS).
∴∠E=∠BAD=90°,CE=AB=6.在Rt△ACE中,由勾股定理，得AE=√(AC² - CE²)=√(10² - 6²)=8.
∴S△ABC=S△ACE=1/2 AE·CE=1/2×8×6=24.故选C.

2. 如图,在$Rt\triangle ABC$中,$\angle ACB = 90^{\circ}$,$AC = 8$,$BC = 6$,$D为线段AB$上一点,连接$CD$,$CD与\angle ABC的平分线BE相交于点F$. 若$\triangle CEF是以EF$为底边的等腰三角形,则$DF$的长为______.

答案：
2.9/5　点拨:如答图,过点E作EG⊥AB于点G.

∵∠ACB=90°,
∴EC⊥BC.又
∵BE平分∠ABC,
∴EG=EC.
∵∠ACB=90°,AC=8,BC=6,
∴AB=10.
∵S△ABE + S△EBC=S△ABC,
∴1/2 AB·EG + 1/2 CB·EC=1/2 AC·BC,即1/2×10·EG + 1/2×6·EC=1/2×8×6.
∴EG=EC=3.
∵△CEF是以EF为底边的等腰三角形,
∴CF=EC=3,
∴∠CEF=∠CFE;又
∵∠DFB=∠CFE,∠CBE=∠ABE,∠CBE + ∠CEF=90°,
∴∠BFD + ∠DBF=90°.
∴∠BDF=90°,
∴CD⊥AB.
∵S△ABC=1/2 AC·BC=1/2 CD·AB,
∴CD=(AC·BC)/AB=24/5.
∴DF=CD - CF=24/5 - 3=9/5.

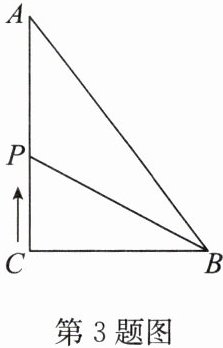
3. 如图,在$\triangle ABC$中,$\angle C = 90^{\circ}$,$AC = 8\ cm$,$BC = 6\ cm$,动点$P从点C$出发,以每秒$1\ cm的速度向终点A$运动,设运动的时间为$t\ s$.
(1)当$t$为何值时,线段$BP把\triangle ABC$的面积平分?
(2)当$t$为何值时,$\triangle ABP$为等腰三角形?
(3)在点$P$的运动过程中,在$AB边上是否存在一点D$,使得$PD + PB$的值最小? 若存在,请求出这个最小值;若不存在,请说明理由.

答案：
3.解:
(1)易知当P为AC边的中点时,线段BP把△ABC 的面积平分，此时t=4.
(2)如答图①,作线段AB的垂直平分线PD,交AC边于点P,垂足为D,则△ABP为等腰三角形.
∵CP=tcm,
∴AP=BP=(8 - t)cm.在Rt△BCP中,由勾股定理,得t² + 6²=(8 - t)²,解得t=7/4.
∴当t为7/4时，△ABP为等腰三角形.

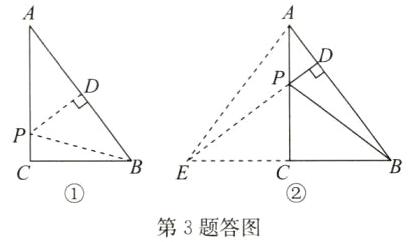
(3)存在.如答图②,作点B关于直线AC的对称点E，过点E作ED⊥AB于点D,交AC于点P,此时PD + PB 的值最小，为ED的长.
∵S△AEB=1/2 BE·AC=1/2 AB·ED,
∴ED=(AC·BE)/AB=(8×12)/10=9.6.
∴PD + PB的最小值为9.6.