2025年启东中学作业本八年级数学上册苏科版宿迁专版第19页解析答案

1. (1)如图①,在 $Rt\triangle ABC$ 中,$\angle BAC = 90^{\circ}$,$AB = AC$,$D$ 为 $BC$ 边上一点(不与点 $B,C$ 重合),将线段 $AD$ 绕点 $A$ 逆时针旋转 $90^{\circ}$ 得到线段 $AE$,连接 $EC$. 求证:$\triangle ABD\cong\triangle ACE$;
(2)如图②,在 $Rt\triangle ABC$ 和 $Rt\triangle ADE$ 中,$\angle BAC= \angle DAE = 90^{\circ}$,$AB = AC$,$AD = AE$,将 $\triangle ADE$ 绕点 $A$ 旋转,使点 $D$ 落在 $BC$ 边上,试探索 $AD^{2}$,$BD^{2}$,$CD^{2}$ 之间满足的数量关系,并证明你的结论.

答案：1.
(1)证明:
∵∠BAC=∠DAE=90°,
∴∠BAC−∠DAC=∠DAE−∠DAC,
　即∠BAD=∠CAE;
在△BAD和△CAE中,$\left\{\begin{array}{l} AB=AC,\\ ∠BAD=∠CAE,\\ AD=AE,\end{array}\right. $
∴△BAD≌△CAE(SAS).
(2)解:$2AD^{2}=BD^{2}+CD^{2}$,理由如下:连接EC.
∵∠BAC=∠DAE=90°,
∴∠BAD=∠CAE.
在△ABD和△ACE中,$\left\{\begin{array}{l} AB=AC,\\ ∠BAD=∠CAE,\\ AD=AE,\end{array}\right. $
∴△ABD≌△ACE(SAS),
∴BD=CE,∠B=∠ACE=45°,
　又
∵∠ACB=∠B=45°,
∴∠BCE=∠ACB+∠ACE=45°+45°=90°,
∴$DE^{2}=CE^{2}+CD^{2}$.
　在Rt△ADE中,$DE^{2}=AD^{2}+AE^{2}=2AD^{2}$,
∴$2AD^{2}=BD^{2}+CD^{2}$.

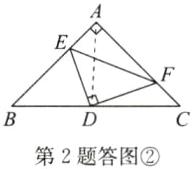
2. 在 $Rt\triangle ABC$ 中,$\angle BAC = 90^{\circ}$,$D$ 是斜边 $BC$ 的中点,$E,F$ 分别是 $AB,AC$ 边上的点,且 $DE\perp DF$,连接 $EF$.
(1)如图①,求证:$\angle BED= \angle AFD$;
(2)如图①,求证:$BE^{2}+CF^{2}= EF^{2}$;
(3)如图②,当 $\angle ABC = 45^{\circ}$ 时,若 $BE = 12$,$CF = 5$,求 $\triangle DEF$ 的面积.

答案：
2.
(1)证明:
∵DE⊥DF,
∴∠EDF=90°.
∵∠BAC=90°,
∴∠AFD+∠AED=180°.
∵∠BED+∠AED=180°,
∴∠BED=∠AFD.
(2)证明:如答图①,延长ED到点P,使DP=DE,连接FP、CP.
　　　　　　　

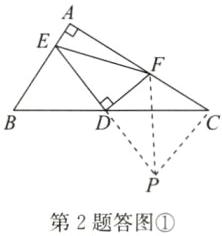
在△BED和△CPD中,$\left\{\begin{array}{l} ED=PD,\\ ∠EDB=∠PDC,\\ BD=CD,\end{array}\right. $
∴△BED≌△CPD(SAS).
∴BE=CP,∠B=∠PCD.
∵∠B+∠ACB=90°,
∴∠ACB+∠DCP=90°,即∠FCP=90°.
在Rt△FCP中,根据勾股定理,得$CF^{2}+CP^{2}=PF^{2}$,
∵BE=CP,PF=EF,
∴$BE^{2}+CF^{2}=EF^{2}$.
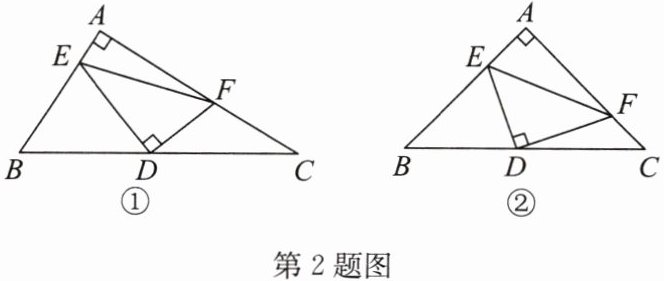
(3)解:如答图②，连接AD.
由题意知△ABC为等腰直角三角形.
∵D为BC边的中点，
∴∠BAD=∠FCD=45°,AD=BD=CD,AD⊥BC,
∴∠ADF+∠FDC=90°.
∵DE⊥DF,
∴∠EDA+∠ADF=90°,
∴∠EDA=∠FDC.
在△AED和△CFD中,$\left\{\begin{array}{l} ∠EAD=∠FCD,\\ AD=CD,\\ ∠ADE=∠CDF,\end{array}\right. $
∴△AED≌△CFD(ASA).
∴AE=CF=5,DE=DF,即△EDF为等腰直角三角形,
∴EF边上的高为$\frac{1}{2}$EF.
由
(2)知$EF^{2}=BE^{2}+CF^{2}=144+25=169$,
∴EF=13.
∴$S_{\triangle DEF}=\frac{1}{2}EF\cdot\frac{1}{2}EF=\frac{1}{4}EF^{2}=\frac{169}{4}$.
　　　　　　