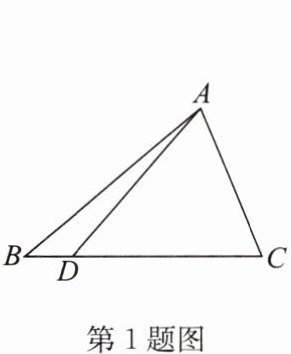
1. 如图,在$\triangle ABC$中,$D是BC$边上的一点,$DC = 5BD = 5$,且$\triangle ADC$的面积为 10,则$\triangle ABC$周长的最小值是( )
A.10
B.12
C.14
D.16
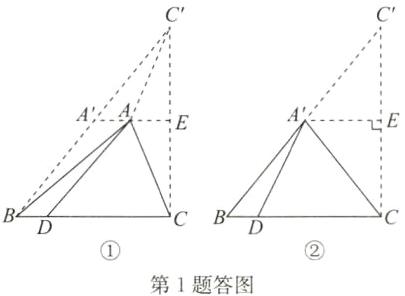
答案:D 点拨:如答图①,过点A作AE//BC,作点C关于直线AE的对称点C',交AE于点E,连接BC',交EA于点A',
∴∠BCC'=90°.
∵DC=5BD=5,
∴BD=1,CD=5,
∴BC=6.
∵S_{△ADC}=10,即$\frac{1}{2}$CD·CE=10,
∴5×CE=20,解得CE=4,
∴C'E=4,
∴CC'=8.
要使△ABC的周长最小,则需点A与点A'重合,即点B,A',C'共线,如答图②,由勾股定理,得BC'^2=6^2+8^2=100,从而BC'=10.
∴△ABC的周长的最小值是A'B+A'C+BC=A'B+A'C'+BC=BC'+BC=10+6=16.故选D.