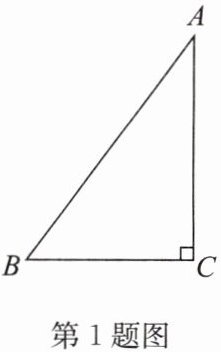
1. 如图,在$\triangle ABC$中,$\angle C= 90^{\circ}$,$AB= 5\mathrm{cm}$,$BC= 3\mathrm{cm}$,若动点$P从点C$开始,按$C→A→B→C$的路径运动,且速度为每秒$1\mathrm{cm}$,设出发的时间为$t\mathrm{s}$.
(1)若点$P出发6.5\mathrm{s}$,求线段$CP和BP$的长;
(2)问$t$满足什么条件时,$\triangle BCP$为直角三角形?
答案:1. 解:
(1)
∵∠C=90°,AB=5cm,BC=3cm,
∴由勾股定理,得AC=4cm.
∴点P出发6.5s,点P在线段AB上且此时有AP=BP=2.5cm,
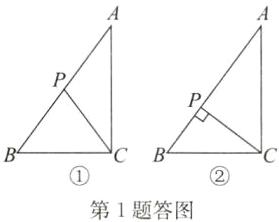
∴P为AB边的中点,如答图①.
根据直角三角形斜边上的中线等于斜边的一半,得CP=$\frac{1}{2}$AB=2.5(cm).
(2)当点P在AC边上运动时,△BCP为直角三角形,此时0<t≤4.
当点P在AB边上,且CP⊥AB时,△BCP为直角三角形,如答图②.
∵$\frac{1}{2}$AB·CP=$\frac{1}{2}$AC·CB,即$\frac{1}{2}$×5CP=$\frac{1}{2}$×4×3,
∴CP=$\frac{12}{5}$cm.
在Rt△APC中,由勾股定理,得AC²=AP²+CP²,
即4²=AP²+($\frac{12}{5}$)²,解得AP=$\frac{16}{5}$.
∴AC+AP=4+$\frac{16}{5}$=$\frac{36}{5}$(cm).
∴t=$\frac{36}{5}$÷1=$\frac{36}{5}$(s).
综上,当0<t≤4或t=$\frac{36}{5}$时,△BCP为直角三角形.