1. 如图,△ABC 与△CDE 都是等边三角形,且点 B,C,D 在同一条直线上,连接 BE,AD,M,N 分别是线段 BE,AD 上的两点,且 BM = $\frac{1}{3}$BE,AN = $\frac{1}{3}$AD,连接 MN,CM,CN,则△CMN 的形状是(
C
)
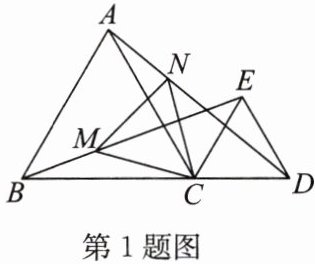
A.等腰三角形
B.直角三角形
C.等边三角形
D.等腰直角三角形
答案:C 点拨:
∵△ABC与△CDE都是等边三角形,
∴AC=BC,EC=DC,∠ACB=∠DCE=60°,
∴∠ACD=∠BCE=120°.
∴△ACD≌△BCE(SAS).
∴AD=BE,∠CAD=∠CBE.
∵BM=$\frac{1}{3}$BE,AN=$\frac{1}{3}$AD,
∴BM=AN.
∴△BCM≌△ACN(SAS).
∴CM=CN,∠BCM=∠ACN.
∴∠MCN=∠ACM+∠ACN=∠ACM+∠BCM=∠ACB=60°,
∴△CMN是等边三角形.故选C.
2. 如图,△ABC 与△CDE 都是等边三角形,当点 B,C,D 在同一条直线上时,连接 AD,BE,交于点 M,连接 CM,试探究线段 BM 与线段 AM,CM 之间的数量关系,并说明理由.
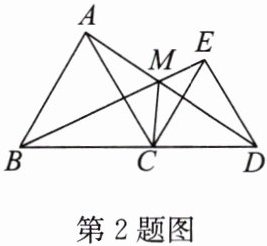
答案:解:BM=AM+CM.理由:如答图,在DA上取点F,使DF=ME,连接CF.
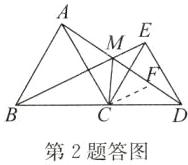
∵△ABC与△CDE都是等边三角形,
∴AC=BC,EC=DC,∠ACB=∠DCE=60°.
∴∠ACD=∠BCE=120°.
∴△ACD≌△BCE(SAS).
∴AD=BE,∠CAD=∠CBE.
∵DF=ME,
∴AD−DF=BE−ME,即AF=BM.同理可证△MCE≌△FCD.
∴CM=CF,∠DCF=∠ECM.
∴∠MCF=∠MCE+∠ECF=∠ECF+∠FCD=∠ECD=60°.
∴△MCF是等边三角形.
∴CM=MF.
∵AF=AM+MF=AM+CM,
∴BM=AM+CM.