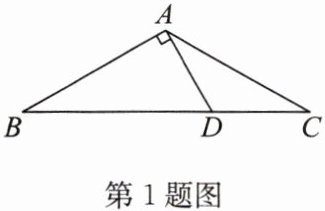
1. 如图,在 $ \triangle ABC $ 中,$ AB = AC $,$ AD \perp AB $ 交 $ BC $ 边于点 $ D $,若 $ \angle BAC = 120^{\circ} $,$ AD = 5 $,则 $ BC $ 的长为 (
15
)
A.7.5
B.10
C.15
D.20
答案:1.C 点拨:
∵AB=AC,∠BAC=120°,
∴∠B=∠C=$\frac{1}{2}$(180°−∠BAC)=30°.
∵AD⊥AB,
∴∠DAB=90°,
∴BD=2AD=10,∠CAD=∠BAC−∠BAD=30°.
∴∠C=∠CAD=30°.
∴CD=AD=5.
∴BC=BD+CD=10+5=15.
2. 在等腰三角形 $ ABC $ 中,$ AD \perp BC $ 交直线 $ BC $ 于点 $ D $,若 $ AD = \frac{1}{2}BC $,则等腰三角形 $ ABC $ 的顶角的度数为______.
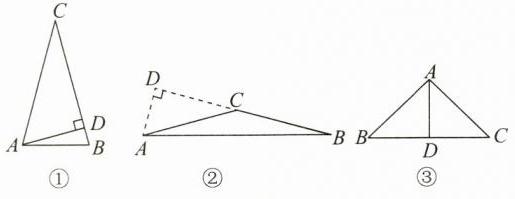
答案:2.30°或150°或90° 点拨:①若BC为腰.
∵AD⊥BC于点D,AD=$\frac{1}{2}$BC,AC=BC,在Rt△ADC中,AD=$\frac{1}{2}$AC,
∴∠ACD=30°.如答图①,AD在△ABC的内部时,顶角∠C=30°;如答图②,AD在△ABC的外部时,顶角∠ACB=180°-30°=150°.②若BC为底,如答图③.
∵AD⊥BC于点D,AD=$\frac{1}{2}$BC,
∴AD=BD=CD.
∴∠B=∠BAD,∠C=∠CAD.
∴∠BAD+∠CAD=$\frac{1}{2}$×180°=90°.
∴顶角∠BAC=90°.综上所述,等腰三角形ABC的顶角度数为30°或150°或90°.
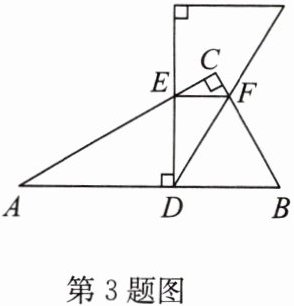
3. 如图,在 $ Rt\triangle ABC $ 中,$ \angle ACB = 90^{\circ} $,$ \angle A = 30^{\circ} $,$ BC = 2 $. 三角尺中 $ 30^{\circ} $ 角的顶点 $ D $ 在边 $ AB $ 上,两边分别与 $ \triangle ABC $ 的边 $ AC $,$ BC $ 相交于点 $ E $,$ F $,且 $ DE $ 始终与 $ AB $ 垂直.
(1)
等边
$ \triangle BDF $ 是______三角形. (填特殊三角形的名称)
(2) 在平移三角尺的过程中,$ AD - CF $ 的值是否发生变化?如果不变,求出 $ AD - CF $ 的值;如果发生变化,请说明理由.
(3) 当平移三角尺使 $ EF // AB $ 时,求 $ AD $ 的长.
答案:3.
(1)等边
(2)解:AD−CF的值不变.
∵∠ACB=90°,∠A=30°,BC=2,
∴AB=2BC=4.
∵BF+CF=2,
∴BF=2−CF;又
∵△BDF是等边三角形,
∴BD=BF=2−CF.
∴AD=4−(2−CF)=2+CF.
∴AD−CF=2+CF−CF=2.
(3)解:
∵EF//AB,
∴∠CEF=∠A=30°,∠FED=∠ADE=90°,
∴在Rt△CEF中,CF=$\frac{1}{2}$EF.
∵在Rt△EFD中,∠EDF=30°,
∴EF=$\frac{1}{2}$DF,
∴CF=$\frac{1}{2}$×$\frac{1}{2}$DF=$\frac{1}{4}$DF.
∴DF=BF=BC−CF=2−CF.
∴CF=$\frac{1}{4}$(2−CF),解得CF=$\frac{2}{5}$.由
(2)知AD−CF=2,
∴AD=2+CF=2+$\frac{2}{5}$=$\frac{12}{5}$.
∴AD的长为$\frac{12}{5}$.