10. 点$P(5,-12)$到原点的距离是
13
.
答案:13
解析:
根据两点间距离公式,点$P(x,y)$到原点$(0,0)$的距离为$\sqrt{x^2 + y^2}$。
对于点$P(5,-12)$,其到原点的距离为:
$\sqrt{5^2 + (-12)^2} = \sqrt{25 + 144} = \sqrt{169} = 13$
13
11. 小亮的体重为$44.85 kg$,若精确到$0.1 kg$,得到的近似值为
44.9
$kg$.
答案:44.9
12. 已知一次函数$y= x+b的图象经过点A(-1,1)$,则$b$的值是
2
.
答案:2
解析:
将点$A(-1,1)$代入$y = x + b$,得$1=-1 + b$,解得$b=2$。
2
13. $A(0,a)$,$B(3,5)$是平面直角坐标系中的两点,线段$AB$长度的最小值为
3
.
答案:3
解析:
$\because A(0,a)$,$B(3,5)$
$\therefore AB=\sqrt{(3-0)^2+(5-a)^2}=\sqrt{9+(5-a)^2}$
$\because (5-a)^2\geq0$
$\therefore$当$5-a=0$,即$a=5$时,$AB$取得最小值
$\therefore AB_{min}=\sqrt{9+0}=3$
3
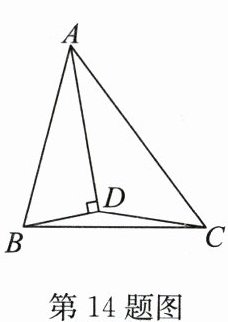
14. 如图,在$\triangle ABC$中,$AD为\angle BAC$的平分线,作$BD\perp AD于点D$,连接$CD$,$\triangle ABC$的面积为8,则$\triangle ACD$的面积为
4
.
答案:4
解析:
证明:延长$BD$交$AC$于点$E$。
∵$AD$平分$\angle BAC$,
∴$\angle BAD=\angle EAD$。
∵$BD\perp AD$,
∴$\angle ADB=\angle ADE=90°$。
在$\triangle ABD$和$\triangle AED$中,
$\begin{cases} \angle BAD=\angle EAD, \\ AD=AD, \\ \angle ADB=\angle ADE, \end{cases}$
∴$\triangle ABD\cong\triangle AED(ASA)$。
∴$BD=ED$,$S_{\triangle ABD}=S_{\triangle AED}$。
∵$BD=ED$,
∴$S_{\triangle BDC}=S_{\triangle EDC}$(等底同高)。
设$S_{\triangle EDC}=x$,则$S_{\triangle BDC}=x$,$S_{\triangle AED}=S_{\triangle ABD}=y$。
∵$S_{\triangle ABC}=S_{\triangle ABD}+S_{\triangle BDC}+S_{\triangle ADC}=y+x+(y+x)=2(y+x)=8$,
∴$y+x=4$。
∵$S_{\triangle ACD}=S_{\triangle AED}+S_{\triangle EDC}=y+x=4$。
4
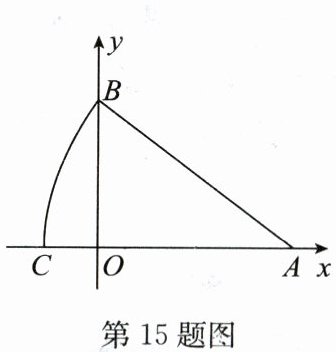
15. 如图,在平面直角坐标系中,$A(8,0)$,$B(0,6)$,以点$A$为圆心,$AB$长为半径画弧,交$x轴的负半轴于点C$,则点$C$的坐标为
(-2,0)
.
答案:(-2,0)
解析:
解:
∵ $ A(8,0) $, $ B(0,6) $,
∴ $ OA=8 $, $ OB=6 $。
在 $ Rt\triangle AOB $ 中,$ AB=\sqrt{OA^2+OB^2}=\sqrt{8^2+6^2}=10 $。
∵ 以点 $ A $ 为圆心,$ AB $ 长为半径画弧,交 $ x $ 轴负半轴于点 $ C $,
∴ $ AC=AB=10 $。
设 $ C(x,0) $,则 $ AC=|8-x|=10 $。
∵ 点 $ C $ 在 $ x $ 轴负半轴,$ x<0 $,
∴ $ 8-x=10 $,解得 $ x=-2 $。
∴ 点 $ C $ 的坐标为 $ (-2,0) $。
$(-2,0)$
16. 在一次函数$y= (k+5)x-2$中,$y随x$的增大而减小,则$k$的取值范围是
k<-5
.
答案:k<-5
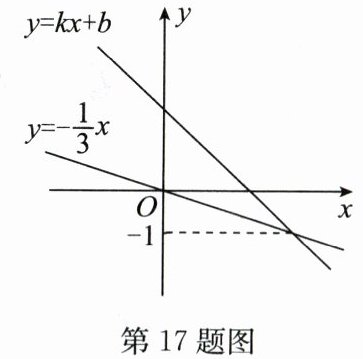
17. 在平面直角坐标系中,一次函数$y= kx+b(k\neq 0,k,b$均为常数)与正比例函数$y= -\frac{1}{3}x$的图象如图所示,则关于$x的不等式kx+b>-\frac{1}{3}x$的解集为
x<3
.
答案:x<3
解析:
解:由图可知,一次函数$y = kx + b$与正比例函数$y=-\frac{1}{3}x$的交点的纵坐标为$-1$。
将$y=-1$代入$y = -\frac{1}{3}x$,得$-1=-\frac{1}{3}x$,解得$x = 3$,即交点坐标为$(3,-1)$。
观察图象,当$x<3$时,一次函数$y = kx + b$的图象在正比例函数$y=-\frac{1}{3}x$的图象上方,所以不等式$kx + b>-\frac{1}{3}x$的解集为$x<3$。
$x<3$
18. 如图,以点阵中的相邻4个点为顶点的小正方形面积为1,则五边形$ABCEF$的面积为
$\frac{131}{30}$
.
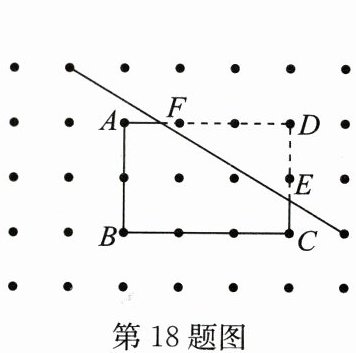
答案:$\frac{131}{30}$
19. (8分)解方程:(1)$2x^{2}-8= 0$; (2)$x^{3}+3= 2$.
答案:
(1)$x_{1}=2,x_{2}=-2$
(2)$x=-1$
20. (8分)计算:$(π-3.14)^{0}+\sqrt{(-2)^{2}}-\sqrt[3]{-27}$.
答案:解:原式=1+2-(-3)=3+3=6.
解析:
解:原式$=1+\sqrt{4}-(-3)$
$=1+2+3$
$=6$
21. (8分)已知一次函数$y= ax-3$,当$x= 1$时,$y= 7$,当$x= -2$时,求$y$的值.
答案:解:由题意得7=a×1-3,解得a=10,
∴y=10x-3. 当x=-2时,y=10×(-2)-3=-23.