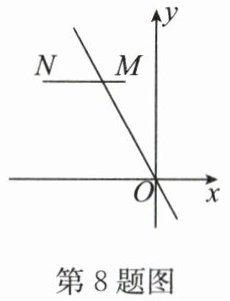
8. 如图,在平面直角坐标系中,$M(-1,3),N(a,3)$,若直线$y = - 2x与线段MN$有公共点,则$a$的取值范围是
a≤-1.5
.
解析:
解:
∵点$M(-1,3)$,$N(a,3)$,
∴线段$MN$在直线$y = 3$上,且$MN// x$轴。
联立$\begin{cases}y = 3 \\ y=-2x\end{cases}$,解得$x=-\dfrac{3}{2}$。
∴直线$y = - 2x$与直线$y = 3$的交点为$\left(-\dfrac{3}{2},3\right)$。
∵直线$y=-2x$与线段$MN$有公共点,
∴交点$\left(-\dfrac{3}{2},3\right)$在线段$MN$上。
当$a < -1$时,线段$MN$的横坐标范围为$[a,-1]$,则$a\leqslant-\dfrac{3}{2}$;
当$a\geqslant-1$时,线段$MN$的横坐标范围为$[-1,a]$,此时$-\dfrac{3}{2} < -1$,交点不在线段上。
综上,$a\leqslant-\dfrac{3}{2}$。
$a\leqslant-1.5$