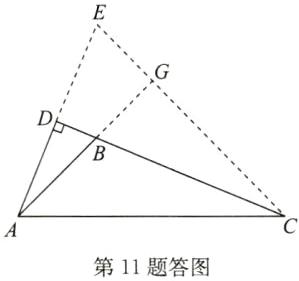
7. 如图,将三角形纸片 $ABC$ 沿 $AD$ 折叠,使点 $C$ 落在 $BD$ 边上的点 $E$ 处.若 $BC = 8$,$BE = 2$,则 $AB^{2}-AC^{2}$ 的值为
16
.
答案：16
解析：
解：设 $DE = x$，由折叠性质得 $DC = DE = x$，$AE = AC$。
因为 $BC = 8$，$BE = 2$，所以 $BD = BE + DE = 2 + x$。
又因为 $BC = BD + DC$，即 $8 = (2 + x) + x$，解得 $x = 3$，故 $DE = DC = 3$，$BD = 5$。
在 $Rt\triangle ABD$ 中，$AB^2 = AD^2 + BD^2$；在 $Rt\triangle AED$ 中，$AE^2 = AD^2 + DE^2$。
所以 $AB^2 - AC^2 = AB^2 - AE^2 = (AD^2 + BD^2) - (AD^2 + DE^2) = BD^2 - DE^2 = 5^2 - 3^2 = 25 - 9 = 16$。
16
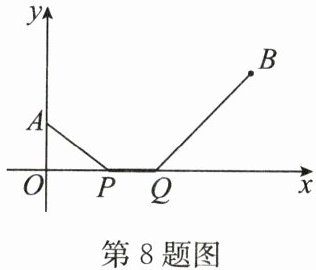
8. 如图,在平面直角坐标系中,已知 $A(0,1)$,$B(4,2)$,$PQ$ 是 $x$ 轴上的一条动线段,且 $PQ = 1$,当 $AP + PQ + QB$ 取最小值时,点 $Q$ 的坐标为
(2,0)
.
答案：(2,0)
解析：
解：作点$A(0,1)$关于$x$轴的对称点$A'(0,-1)$，将点$B(4,2)$向左平移$1$个单位得到点$B'(3,2)$。
连接$A'B'$，设直线$A'B'$的解析式为$y = kx + b$。
将$A'(0,-1)$，$B'(3,2)$代入，得$\begin{cases}b=-1\\3k + b=2\end{cases}$，解得$\begin{cases}k=1\\b=-1\end{cases}$，即$y = x - 1$。
直线$A'B'$与$x$轴交于点$P$，令$y = 0$，则$x - 1 = 0$，解得$x = 1$，即$P(1,0)$。
因为$PQ = 1$且$Q$在$x$轴上$P$右侧，所以$Q(2,0)$。
(2,0)
9. (14 分)求下列各式中 $x$ 的值.
(1)$5x^{2}-10 = 0$;
(2)$x^{3}-2 = 6$.
答案：
(1)$x_{1}=\sqrt{2},x_{2}=-\sqrt{2}$
(2)2
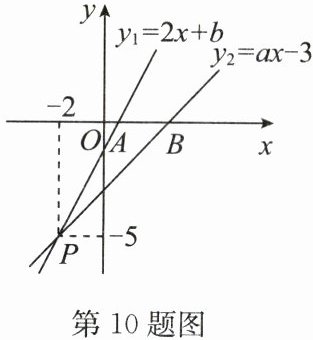
10. (15 分)(2024·宿迁期末)如图,已知函数 $y_{1}= 2x + b$ 和 $y_{2}= ax - 3$ 的图象交于点 $P(-2,-5)$,这两个函数的图象与 $x$ 轴分别交于点 $A,B$.
(1)求这两个函数的表达式;
(2)求$\triangle ABP$的面积;
(3)根据图象直接写出不等式 $2x + b＞ax - 3$ 的解集.
答案：解:
(1)将(-2,-5)代入$y_{1}=2x+b$,得$-5=2×(-2)+b$,解得$b=-1$,从而$y_{1}=2x-1$.将(-2,-5)代入$y_{2}=ax-3$,得$-5=-2a-3$,解得$a=1$,从而$y_{2}=x-3$.
∴这两个函数的表达式分别为$y_{1}=2x-1$和$y_{2}=x-3$.
(2)在$y_{1}=2x-1$中,令$y=0$,得$x=\frac{1}{2}$.
∴$A\left( \frac{1}{2},0 \right)$.在$y_{2}=x-3$中,令$y=0$,得$x=3$,
∴$B(3,0)$.
∴$S_{\triangle ABP}=\frac{1}{2}AB×5=\frac{1}{2}×\frac{5}{2}×5=\frac{25}{4}$.
(3)$x＞-2$.
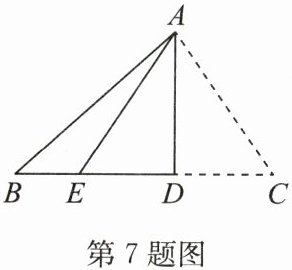
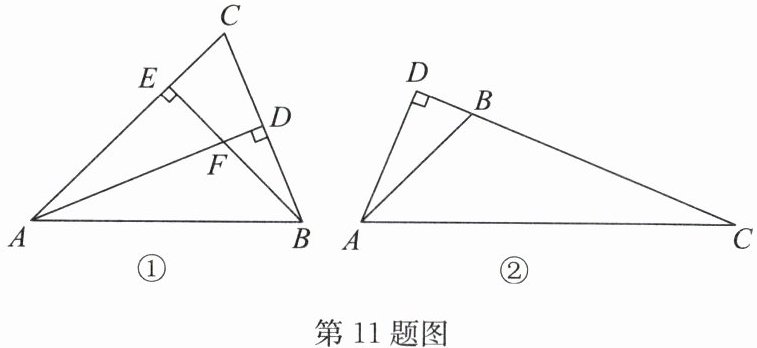
11. (15 分)(2024·宿城期中)【探索发现】如图①,已知在$\triangle ABC$中,$\angle BAC = 45^{\circ}$,$AD\perp BC$,垂足为 $D$,$BE\perp AC$,垂足为 $E$,$AD$ 与 $BE$ 相交于点 $F$.
(1)线段 $AF$ 与 $BC$ 的数量关系:$AF$______$BC$(用“$＞$”“$＜$”或“$=$”填空);
(2)若$\angle ABC = 67.5^{\circ}$,试猜想线段 $AF$ 与 $BD$ 有何数量关系,并说明理由;
【拓展应用】(3)如图②,在$\triangle ABC$ 中,$AD\perp BC$,交 $BC$ 的延长线于点 $D$,$\angle BAC = 45^{\circ}$,$\angle C = 22.5^{\circ}$,$AD = 3$,求$\triangle ABC$的面积.
答案：(1)=
(2)解:$AF=2BD$,理由:
∵$AD\perp BC$,$BE\perp AC$,
∴$\angle AEF=\angle BEC=\angle BDF=90°$.又$\angle AFE=\angle DFB$,
∴$\angle EAF=\angle EBC$.
∵$BE\perp AC$,$\angle BAC=45°$,
∴$\triangle ABE$是等腰直角三角形,
∴$AE=BE$,
∴$\triangle AEF\cong\triangle BEC(ASA)$,
∴$AF=BC$.
∵$\angle BAC=45°$,$\angle ABC=67.5°$,
∴$\angle C=\angle ABC=67.5°$.
∴$AB=AC$.又
∵$AD\perp BC$,
∴$BC=2BD$,
∴$AF=2BD$.
(3)解:如答图,延长$AD$至点$E$,使$DE=AD$,连接$CE$,延长$AB$交$CE$于点$G$.由
(2)知$BC=AE=2AD=6$,
∴$S_{\triangle ABC}=\frac{1}{2}BC× AD=\frac{1}{2}×6×3=9$.
