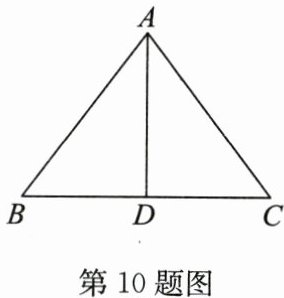
10. (12 分)如图,$AD是\triangle ABC$的中线,$AB = 20,BC = 24,AD = 16$.求$AC$的长.
答案:解:
∵AD是△ABC的中线,BC=24,
∴BD=1/2BC=12.
∵AB=20,AD=16,
∴AD²+BD²=16²+12²=400,AB²=20²=400.
∴AD²+BD²=AB².
∴∠ADB=90°.
∴AD垂直平分BC,
∴AC=AB=20.
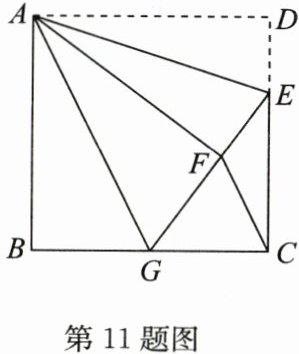
11. (15 分)如图,在正方形$ABCD$中,$AB = 6$,点$E在边CD$上,且$CD = 3DE$,将$\triangle ADE沿AE对折至\triangle AFE$,延长$EF交边BC于点G$,连接$AG,CF$.
(1)求证:$\triangle ABG\cong\triangle AFG$;
(2)求$BG$的长;
(3)求$\triangle FEC$的面积.
答案:(1)证明:
∵△AFE是由△ADE折叠得到的,
∴AF=AD,∠AFE=∠AFG=∠D=90°.又
∵四边形ABCD是正方形,
∴AB=AD,∠B=∠D,
∴AB=AF,∠B=∠AFG=90°.在Rt△ABG和Rt△AFG中,{AG=AG,AB=AF,
∴Rt△ABG≌Rt△AFG(HL).(2)解:在正方形ABCD中,AB=6,CD=3DE,
∴EF=DE=1/3CD=2,CE=CD-DE=4.由
(1)知△ABG≌△AFG,
∴BG=FG.设BG=FG=x,则CG=6-x,EG=2+x.在Rt△ECG中,根据勾股定理得(6-x)²+4²=(x+2)²,解得x=3.
∴BG=3.(3)解:由
(2)知,EF=2,BG=FG=3,
∴EG=EF+FG=5,CG=BC-BG=3,
∴S△CEG=1/2CG·CE=1/2×3×4=6,
∴S△FEC=2/5S△CEG=2/5×6=12/5.
12. (15 分)(2024·宿豫期末)一辆快车从甲地驶往乙地,一辆慢车从乙地驶往甲地,两车同时出发,匀速行驶,两车在途中相遇时,快车恰巧出现故障,慢车继续驶往甲地,快车维修好后按原速继续驶往乙地,两车到达各自终点后停止,两车之间的距离$y(km)与慢车行驶的时间x(h)$之间的关系如图所示.
(1)甲、乙两地之间的距离为______$km$;
(2)求快车和慢车的速度,并直接写出点$E$的坐标;
(3)求$AB,CD$所在直线对应的函数表达式;
(4)慢车出发多少小时后,两车相距$300 km$?
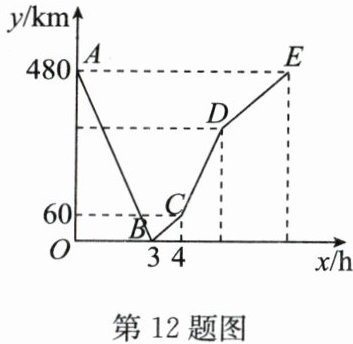
(1)
480
(2)
解:由题可知BC段只有慢车在行驶,则慢车的速度为60÷(4-3)=60(km/h),AB表示两车从开始到相遇的过程,则两车的速度和为480÷3=160(km/h),
∴快车的速度为160-60=100(km/h).
∵慢车到达终点所用的时间为480÷60=8(h),
∴点E的坐标为(8,480).
(3)
解:由题知,CD表示快车修好开始行驶至终点,(480-3×100)÷100=1.8(h),1.8×160+60=348(km),4+1.8=5.8(h),从而D(5.8,348),由题图知,A(0,480),B(3,0),C(4,60).设AB所在直线的函数表达式为y=k₂x+480,则3k₁+480=0,解得k₁=-160,
∴AB所在直线的函数表达式为y=-160x+480.设CD所在直线的函数表达式为y=k₂x+b,则有{4k₂+b=60,5.8k₂+b=348,解得{k₂=160,b=-580,
∴CD所在直线的函数表达式为y=160x-580.
(4)
解:由D(5.8,348)知,两车相距300 km在AB段和CD段.把y=300代入y=-160x+480,得x=1.125;把y=300代入y=160x-580,得x=5.5.
∴慢车出发1.125 h或5.5 h后,两车相距300 km.
答案:(1)480(2)解:由题可知BC段只有慢车在行驶,则慢车的速度为60÷(4-3)=60(km/h),AB表示两车从开始到相遇的过程,则两车的速度和为480÷3=160(km/h),
∴快车的速度为160-60=100(km/h).
∵慢车到达终点所用的时间为480÷60=8(h),
∴点E的坐标为(8,480).(3)解:由题知,CD表示快车修好开始行驶至终点,(480-3×100)÷100=1.8(h),1.8×160+60=348(km),4+1.8=5.8(h),从而D(5.8,348),由题图知,A(0,480),B(3,0),C(4,60).设AB所在直线的函数表达式为y=k₂x+480,则3k₁+480=0,解得k₁=-160,
∴AB所在直线的函数表达式为y=-160x+480.设CD所在直线的函数表达式为y=k₂x+b,则有{4k₂+b=60,5.8k₂+b=348,解得{k₂=160,b=-580,
∴CD所在直线的函数表达式为y=160x-580.(4)解:由D(5.8,348)知,两车相距300 km在AB段和CD段.把y=300代入y=-160x+480,得x=1.125;把y=300代入y=160x-580,得x=5.5.
∴慢车出发1.125 h或5.5 h后,两车相距300 km.