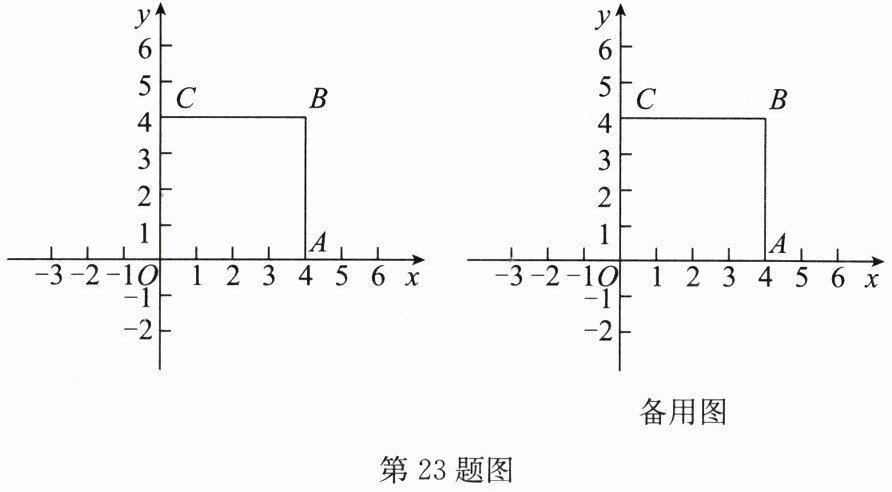
23. (10分)如图,正方形 $ OABC $ 的边长为 4,边 $ OA $,$ OC $ 分别在 $ x $ 轴、$ y $ 轴上.
(1)把正方形 $ OABC $ 先向右平移 2 个单位长度,再向上平移 1 个单位长度,得到正方形 $ O'A'B'C' $,在图中画出正方形 $ O'A'B'C' $,并写出点 $ B $ 的对应点 $ B' $ 的坐标;
(2)规定:若 $ a $,$ b $ 为整数,则点 $ (a,b) $ 称为整点,如点 $ (0,4) $ 为整点.求正方形 $ OABC $ 与正方形 $ O'A'B'C' $ 重叠区域(包括边界)内的整点个数;
(3)若点 $ P $ 在 $ x $ 轴上方,以 $ O $,$ A $,$ P $ 为顶点的三角形是以 $ OA $ 为腰的等腰三角形,且 $ \triangle OAP $ 的面积为 2,请求出所有符合条件的点 $ P $ 的坐标.
答案:解:
(1)如答图,正方形O'A'B'C'即为所求,点B'的坐标为(6,5).
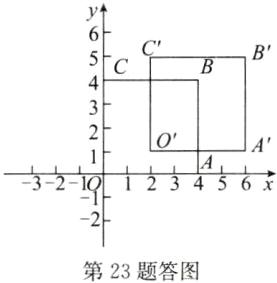
(2)正方形OABC与正方形O'A'B'C'重叠区域(包括边界)内的整点有(2,1),(3,1),(4,1),(2,2),(3,2),(4,2),(2,3),(3,3),(4,3),(2,4),(3,4),(4,4),
∴正方形OABC与正方形O'A'B'C'重叠区域(包括边界)内的整点有12个.
(3)设点P的坐标为(m,n),
∵点P在x轴上方,
∴n>0.由题意知OA=4.
∵△OAP的面积为2,
∴1/2 OA·n=2,即1/2×4·n=2,解得n=1. 当OA=OP=4时,有m²+1²=4²,
∴m=±√15.
∴点P的坐标为(√15,1)或(-√15,1). 当OA=PA=4时,(m-4)²+1²=4²,
∴m=4±√15.
∴点P的坐标为(4+√15,1)或(4-√15,1). 综上所述,点P的坐标为(√15,1)或(-√15,1)或(4+√15,1)或(4-√15,1).