2025年启东中学作业本八年级数学上册苏科版宿迁专版第97页解析答案

8. 用含边数 $ n $ 的式子表示多边形的内角和 $ S $,其关系式为

$S=(n-2)\cdot 180^{\circ}$

,其中变量是

$S$和$n$

,常量是

$-2$和$180^{\circ}$

答案：$S=(n-2)\cdot 180^{\circ}$ $S$和$n$ $-2$和$180^{\circ}$

9. 已知函数：① $ y = (\sqrt{x})^{2} $；② $ y = |x| $；③ $ y = \frac{x^{2}}{x} $；④ $ y = \sqrt[3]{x^{3}} $. 其中,与 $ y = x $ 表示同一函数的是

④

.(填序号)

答案：④

10. 按如图所示的运算程序,输入一个实数 $ x $,便可以输出一个相应的实数 $ y $. $ y $ 是 $ x $ 的函数吗？请说明理由.

答案：解:$y$是$x$的函数.理由如下:
由题意得$y=2(x-3)+4$,因为在这个变化过程中有两个变量$x$和$y$,对于$x$的每一个值,$y$都有唯一的值与它对应,所以$y$是$x$的函数,其中$x$是自变量,$y$是因变量.

11. 如图是用棋子摆成的“上”字：

如果按照以上规律继续摆下去,那么通过观察,可以发现：
(1)第 4 个、第 5 个“上”字分别需用

和

枚棋子；
(2)第 $ n $ 个“上”字需用

$4n+2$

枚棋子.

答案：
(1)18 22
(2)$4n+2$

12. 如图①,在 $ \triangle ABC $ 中,$ BC = 6 $,$ AF $ 为 $ BC $ 边上的高,$ P $ 是 $ BC $ 上一动点,沿 $ BC $ 由点 $ B $ 向点 $ C $ 运动,连接 $ AP $,在这个变化过程中设 $ BP = x $,且把 $ x $ 看成自变量.
(1)图中哪个三角形的面积可以看成因变量？
(2)设 $ \triangle APC $ 的面积为 $ S $,图②刻画的是 $ S $ 随 $ x $ 变化而变化的图象,根据图象回答以下问题：
①图中点 $ M $ 代表的意义是

$BP=1$时,$\triangle APC$的面积为 10

；② $ \triangle ABC $ 的高 $ AF = $

；
③ $ S $ 与 $ x $ 的关系式是

$S=12-2x$

；④ $ a $ 的值为

.
(3)设 $ \triangle ABP $ 的面积为 $ y $,写出 $ y $ 与 $ x $ 的关系式,并求当 $ x $ 为何值时,$ \triangle APC $ 的面积与 $ \triangle ABP $ 的面积相等？

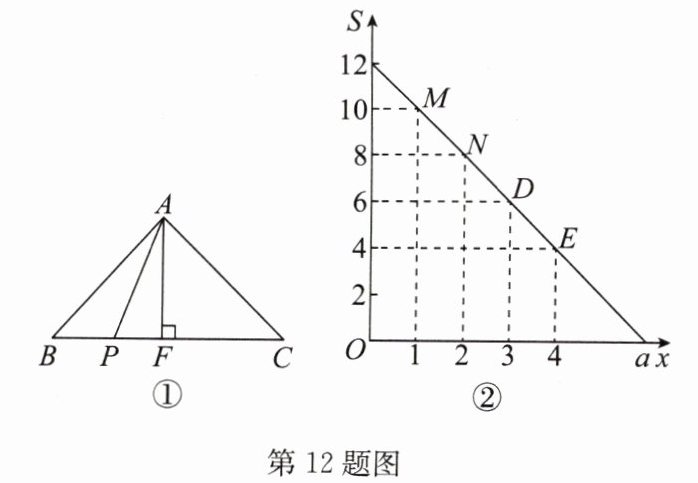
(1)解:$\triangle ABP$,$\triangle APC$,$\triangle APF$.
(3)解:$y=\frac{1}{2}BP\cdot AF=2x$,当$y=S$时,$\triangle APC$的面积与$\triangle ABP$的面积相等,即$12-2x=2x$,解得$x=3$,故当$x=3$时,$\triangle APC$的面积与$\triangle ABP$的面积相等.

答案：
(1)解:$\triangle ABP$,$\triangle APC$,$\triangle APF$.
(2)①$BP=1$时,$\triangle APC$的面积为 10 ②4
③$S=12-2x$ ④6
(3)解:$y=\frac{1}{2}BP\cdot AF=2x$,当$y=S$时,$\triangle APC$的面积与$\triangle ABP$的面积相等,即$12-2x=2x$,解得$x=3$,故当$x=3$时,$\triangle APC$的面积与$\triangle ABP$的面积相等.