1. (2024·无锡二模)函数 $ y = \frac{2x}{x - 3} $ 中自变量 $ x $ 的取值范围是(
D
)
A.$ x > 3 $
B.$ x \geq 3 $
C.$ x \neq 3 $ 且 $ x \neq 0 $
D.$ x \neq 3 $
答案:D
解析:
要使函数 $ y = \frac{2x}{x - 3} $ 有意义,分母不能为零,即 $ x - 3 \neq 0 $,解得 $ x \neq 3 $。
D
2. 下列图象不能体现 $ y $ 是 $ x $ 的函数的是(
C
)
]

答案:C
解析:
根据函数定义:对于x的每一个确定的值,y都有唯一确定的值与其对应。
选项A、B、D中,任意一条垂直于x轴的直线与图象最多有一个交点,符合函数定义。
选项C中,存在一条垂直于x轴的直线与图象有两个交点,不符合函数定义。
结论:不能体现y是x的函数的是C。
C
3. (2024·武威)已知函数 $ y = - 2x + 4 $,当自变量 $ x > 2 $ 时,函数 $ y $ 的值可以是
-2(答案不唯一)
(写出一个合理的值即可).
答案:-2(答案不唯一)
4. 直角三角形的两个锐角分别为 $ x^{\circ} $和 $ y^{\circ} $,则 $ y $ 与 $ x $ 的函数关系式为
y=90-x
,其中自变量 $ x $ 的取值范围是
0<x<90
.
答案:y=90-x 0<x<90
5. 某天小明骑自行车上学,途中因自行车发生故障,修车耽误了一段时间后继续骑行,按时赶到了学校. 如图是小明从家到学校这一过程中离家的距离 $ s $(米)与时间 $ t $(分)之间的关系.
(1)小明从家到学校的路程共
2000
米,从家出发到学校,小明共用了
20
分钟;
(2)小明修车用了多长时间?
解:小明修车用了15-10=5(分).
(3)小明修车前和修车后的平均速度分别是多少?
解:由题图得,小明修车前的平均速度为1000÷10=100(米/分), 修车后的平均速度为(2000-1000)÷(20-15)=200(米/分).
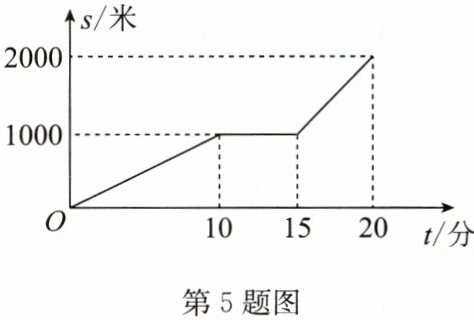
答案:
(1)2000 20
(2)解:小明修车用了15-10=5(分).
(3)解:由题图得,小明修车前的平均速度为1000÷10=100(米/分), 修车后的平均速度为(2000-1000)÷(20-15)=200(米/分).
6. (2024·江西)将常温中的温度计插入一杯 $ 60^{\circ}C $ 的热水(恒温)中,温度计的读数 $ y(^{\circ}C) $ 与时间 $ x(min) $ 的关系用图象可近似表示为(
C
)
]

答案:C
解析:
将常温中的温度计插入$60^{\circ}C$的恒温热水中,温度计读数$y(^{\circ}C)$初始值低于$60^{\circ}C$,随时间$x(min)$增加逐渐升高,最终接近$60^{\circ}C$并趋于稳定。
A选项为直线上升,不符合温度升高速度逐渐减慢的实际情况;
B选项上升速度越来越快,不符合实际;
C选项温度从低于$60^{\circ}C$开始,先快速上升后趋于平缓接近$60^{\circ}C$,符合规律;
D选项温度先升后降,与恒温热水条件矛盾。
结论:C