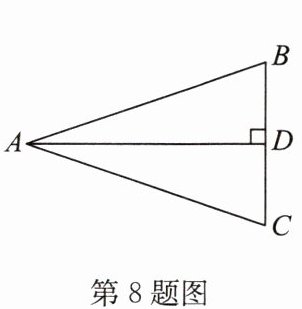
8. 如图,在$\triangle ABC$中,$AD\perp BC$于点D,且AD平分$\angle BAC$.
(1)证明$\triangle ABD\cong\triangle ACD$的依据是“
ASA
”,根据全等可证明$\angle B= \angle C$的依据是______
全等三角形的对应角相等
;
(2)若$\triangle ABC$的周长为36,$\triangle ADC$的周长为30,则$AD= $
12
.
答案:
(1)ASA 全等三角形的对应角相等
(2)12
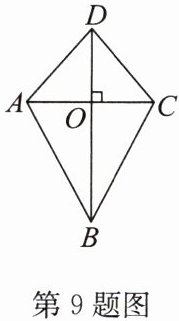
9. 如图,在四边形ABCD中,DB平分$\angle ADC$,$AC\perp BD$,垂足为O.有下列结论:①$AD= CD$;②$AB= CB$;③$AB// CD$;④图中有3对全等三角形.其中正确结论的序号是
①②④
.
答案:①②④
解析:
证明:
∵DB平分∠ADC,
∴∠ADO=∠CDO.
∵AC⊥BD,
∴∠AOD=∠COD=90°.
在△AOD和△COD中,
$\left\{\begin{array}{l} ∠ADO=∠CDO,\\ OD=OD,\\ ∠AOD=∠COD,\end{array}\right.$
∴△AOD≌△COD(ASA),
∴AD=CD,OA=OC,故①正确.
在△AOB和△COB中,
$\left\{\begin{array}{l} OA=OC,\\ ∠AOB=∠COB=90°,\\ OB=OB,\end{array}\right.$
∴△AOB≌△COB(SAS),
∴AB=CB,故②正确.
由△AOD≌△COD,△AOB≌△COB,可得△ABD≌△CBD(SSS),
∴全等三角形有△AOD≌△COD,△AOB≌△COB,△ABD≌△CBD,共3对,故④正确.
AB//CD无法证明,故③错误.
正确结论的序号是①②④.
①②④
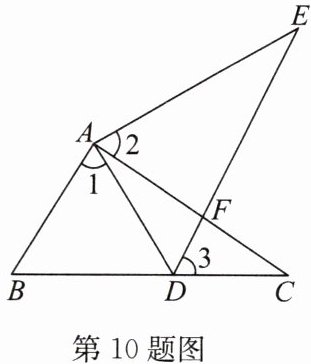
10. 如图,点E在$\triangle ABC$的外部,点D在边BC上,DE交AC于点F,且$\angle 1= \angle 2= \angle 3$,$AE= AC$.求证:$BC= DE$.
答案:证明:
∵在△AFE和△DFC中,∠2=∠3,∠AFE=∠DFC,
∴∠C=∠E.
∵∠1=∠2,
∴∠1+∠DAC=∠2+∠DAC,
即∠BAC=∠DAE.
在△ABC和△ADE中,
∠BAC=∠DAE,
AC=AE,
∠C=∠E,
∴△ABC≌△ADE(ASA).
∴BC=DE.
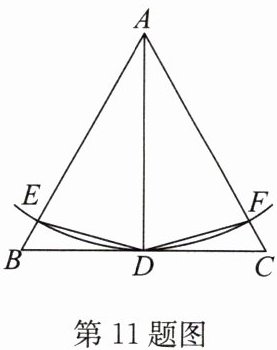
11. 如图,AD是$\triangle ABC$的角平分线,以点A为圆心,AD长为半径画弧,与AB,AC分别交于点E,F,连接DE,DF,且$\angle BDE= \angle CDF$.求证:$BD= CD$.
答案:证明:
∵AD是△ABC的角平分线,
∴∠BAD=∠CAD.
∵以点A为圆心,AD长为半径画弧,与AB,AC分别交于点E,F,
∴AE=AF=AD.
在△ADE和△ADF中,
AE=AF,
∠DAE=∠DAF,
AD=AD,
∴△ADE≌△ADF(SAS).
∴∠ADE=∠ADF.
又
∵∠BDE=∠CDF,
∴∠ADE+∠BDE=∠ADF+∠CDF,
即∠ADB=∠ADC.
又
∵∠BAD=∠CAD,AD=AD,
∴△ADB≌△ADC(ASA).
∴BD=CD.
12. 如图,在$\triangle ABC$中,AE平分$\angle BAC$,$BE\perp AE$,$DE// AC$,且$\angle BAE= 36^{\circ}$,求$\angle BED$的度数.
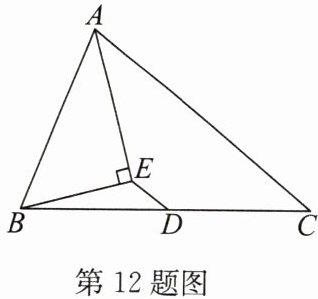
答案:解:如答图,延长BE交AC于点F.
∵AE平分∠BAC,
∴∠BAE=∠FAE.
∵BE⊥AE,
∴∠AEB=∠AEF=90°.
∵∠BAE=36°,
∴∠ABE=90°−∠BAE=90°−36°=54°.
在△AEB和△AEF中,
∠BAE=∠FAE,
AE=AE,
∠AEB=∠AEF,
∴△AEB≌△AEF(ASA).
∴∠AFE=∠ABE=54°.
∴∠BFC=180°−54°=126°.
∵DE//AC,
∴∠BED=∠BFC=126°.