8. 在四边形$ABCD$中,$\angle A = \angle B = \angle C = \angle D = 90^{\circ}$,$AB = CD = 10$,$BC = AD = 8$.
(1)$P为BC$边上一点,将$\triangle ABP沿直线AP翻折至\triangle AEP$的位置.(点$B落在点E$处)
①当点$E落在边CD$上时,利用尺规作图,在图①中作出满足的图形(即$\triangle AEP$的位置,不写作法,保留作图痕迹),并写出此时$DE = $______;
②如图②,$PE与CD相交于点F$,$AE与CD相交于点G$,且$FC = FE$,求$BP$的长.
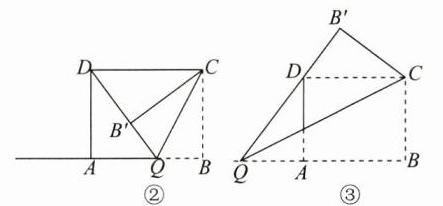
(2)如图③,已知$Q为射线BA$上的一个动点,将$\triangle BCQ沿直线CQ$翻折,使点$B恰好落在直线DQ上的点B'$处,求$BQ$的长.
答案:解:
(1)①6 如答图①.
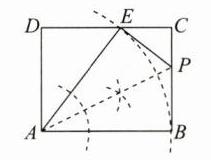
②设BP=x,由翻折可知PE=BP=x.
∵∠C=∠E=90°,EF=CF,∠GFE=∠CFP,
∴△EFG≌△CFP(ASA).
∴GF=PF,GE=CP=8−x,
∴CG=PE=BP=x.
∴DG=10−x,AG=AE−GE=10−(8−x)=x+2.
在Rt△AGD中,由勾股定理,得8²+(10−x)²=(x+2)²,解得x=$\frac{20}{3}$.
∴BP的长为$\frac{20}{3}$.
(2)设BQ=y.如答图②,当点Q在线段AB上时.
∵B'C=BC=8,CD=10,∠CB'Q=∠B=90°,
∴∠DB'C=90°,
∴在Rt△CB'D中,由勾股定理得DB'²=10²−8²=36,
∴DB'=6,
∴DQ=DB'+QB'=6+y
∵AQ=10−y,
∴在Rt△ADQ中,由勾股定理,得8²+(10−y)²=(y+6)²,解得y=4.
如答图③,当点Q在线段BA的延长线上时.
∵B'C=BC=8,CD=10,∠B'=∠B=90°,
∴在Rt△CB'D中,由勾股定理得DB'²=10²−8²=36,
∴DB'=6,
∴DQ=QB'−DB'=y−6,AQ=y−10.
在Rt△ADQ中,由勾股定理,得8²+(y−10)²=(y−6)²,解得y=16.
综上,BQ的长为4或16.