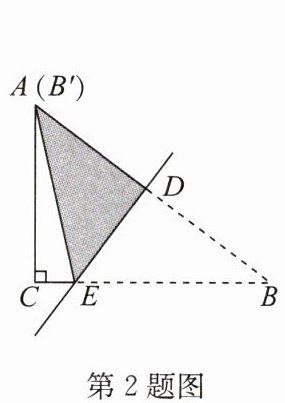
2. 如图,在$\triangle ABC$中,$\angle C = 90^{\circ}$,$AC = 6$,$BC = 8$,$D$,$E分别是斜边AB和直角边CB$上的点,把$\triangle ABC沿着直线DE$折叠,顶点$B的对应点是点B'$,如果点$B'和顶点A$重合,则$CE$的长为(
C
)
A.$2$
B.$6$
C.$\frac{7}{4}$
D.$\frac{55}{16}$
解析:
解:设$CE = x$,则$BE = BC - CE = 8 - x$。
由折叠性质得:$AE = BE = 8 - x$。
在$\triangle ACE$中,$\angle C = 90^{\circ}$,$AC = 6$,根据勾股定理得:$AC^{2} + CE^{2} = AE^{2}$,即$6^{2} + x^{2} = (8 - x)^{2}$。
展开得:$36 + x^{2} = 64 - 16x + x^{2}$。
化简得:$36 = 64 - 16x$。
解得:$16x = 28$,$x = \frac{28}{16} = \frac{7}{4}$。
$\therefore CE = \frac{7}{4}$。
C