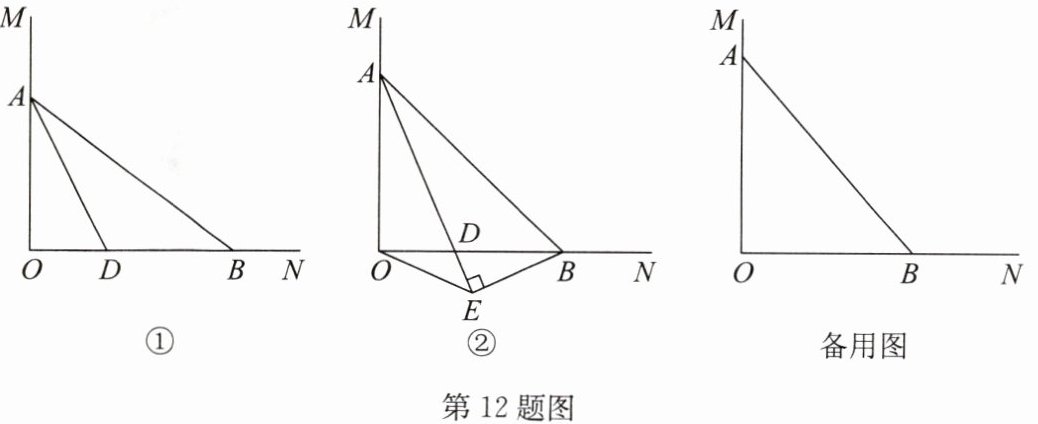
12. 已知 $ \angle MON = 90^{\circ} $,有一根长为 10 的木棒 $ AB $ 的两个端点 $ A $,$ B $ 分别在射线 $ OM $,$ ON $ 上滑动,$ \angle OAB $ 的平分线 $ AD $ 交 $ OB $ 于点 $ D $.
(1)如图①,若 $ OA = 6 $,则 $ OB = $______,$ OD = $______;
(2)如图②,过点 $ B $ 作 $ BE \perp AD $,交 $ AD $ 的延长线于点 $ E $,连接 $ OE $,在 $ AB $ 滑动的过程中,猜想线段 $ OE $,$ BE $ 有何数量关系,并说明理由;
(3)在 $ AB $ 滑动的过程中,$ \triangle AOB $ 面积的最大值为______.
]
答案:(1)8 3
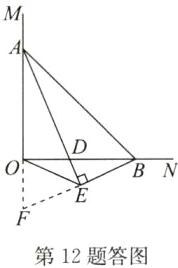
(2)解:OE=BE;理由:如答图,延长AO和BE,交于点F,则∠AEB=∠AEF=∠BOF=90°,
又
∵AD平分∠OAB,
∴∠EAF=∠EAB.
又
∵AE=AE,
∴△AEB≌△AEF(ASA),
∴BE=EF;又
∵∠BOF=90°,
∴OE=$\frac{1}{2}$BF=BE.
(3)25