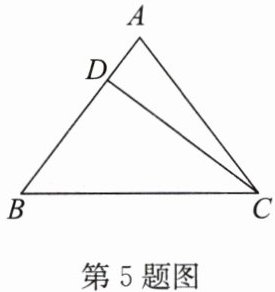
5. 如图,$ \triangle ABC $ 中,$ AB = AC = 5 $,$ BC = 6 $,$ D $ 是 $ AB $ 边上的一个动点,求线段 $ CD $ 的最小值.
答案:解:如答图,过点A作AE⊥BC于点E,当CD⊥AB于点D时,CD最小.
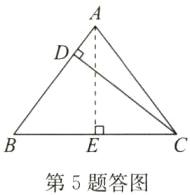
∵AB=AC=5,BC=6,AE⊥BC,
∴BE=$\frac{1}{2}$BC=3,
∴AE=$\sqrt{5^{2}-3^{2}}$=4.
∵S△ABC=$\frac{1}{2}$BC·AE=$\frac{1}{2}$AB·CD,
∴CD=$\frac{BC·AE}{AB}$=$\frac{6×4}{5}$=$\frac{24}{5}$.
∴线段CD的最小值为$\frac{24}{5}$.