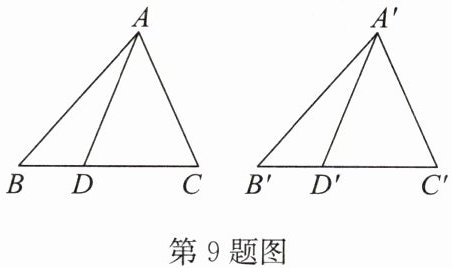
9. 如图,在△ABC和△A′B′C′中,点D,D′分别在BC,B′C′上,且△ABC≌△A′B′C′,BD= B′D′.求证:AD= A′D′.
答案:证明:
∵△ABC≌△A'B'C',
∴AB=A'B',∠B=∠B'.
又
∵BD=B'D',
∴△ABD≌△A'B'D'(SAS).
∴AD=A'D'.
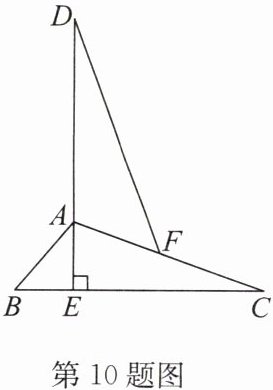
10. 如图,在△ABC中,∠B= 50°,∠C= 20°.过点A作AE⊥BC,垂足为E,延长EA至点D,使AD= AC.在边AC上截取AF= AB,连接DF.求证:DF= CB.
答案:证明:在△ABC中,
∵∠B=50°,∠C=20°,
∴∠CAB=180°-∠B-∠C=110°.
∵AE⊥BC,
∴∠AEC=90°,
∴∠DAF=∠AEC+∠C=110°,
∴∠DAF=∠CAB.
在△DAF和△CAB中,$\left\{\begin{array}{l} AD=AC,\\ ∠DAF=∠CAB,\\ AF=AB,\end{array}\right. $
∴△DAF≌△CAB(SAS).
∴DF=CB.
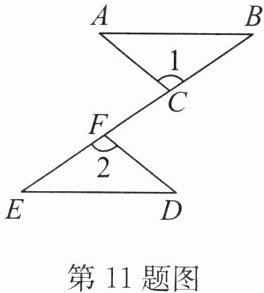
11. 如图,点C,F在线段BE上,BF= EC,∠1= ∠2,AC= DF.
求证:(1)△ABC≌△DEF;(2)AB//DE.
答案:
(1)
∵BF=EC,
∴BF-CF=EC-CF,即BC=EF.
又
∵∠1=∠2,AC=DF,
∴△ABC≌△DEF(SAS).
(2)
∵△ABC≌△DEF,
∴∠B=∠E,
∴AB//DE.