1. 根据下列条件,能画出唯一确定的△ABC的是(
D
)
A.∠A= 45°
B.AB= 5,∠A= 45°
C.∠A= ∠B= ∠C= 60°
D.AB= 5,∠B= 45°,BC= 3
答案:D
解析:
A.仅∠A=45°,无法确定三角形的大小和形状,不唯一;
B.AB=5,∠A=45°,仅一边一角,无法确定三角形唯一,不唯一;
C.∠A=∠B=∠C=60°,等边三角形但边长不确定,不唯一;
D.AB=5,∠B=45°,BC=3,符合“两边及其夹角”(SAS)判定定理,能画出唯一确定的三角形。
D
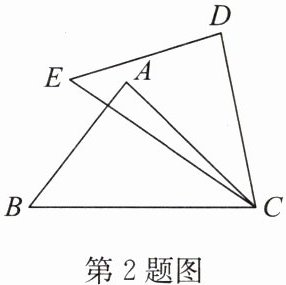
2. (2025·吴江区期中)如图,在△ABC和△DEC中,∠ACD= ∠BCE,已知AC= DC,小亮说:若BC= EC,则可判定△ABC≌△DEC,他的依据是
SAS
.
答案:SAS
解析:
证明:
∵∠ACD=∠BCE,
∴∠ACD+∠ACE=∠BCE+∠ACE,即∠ACB=∠DCE。
在△ABC和△DEC中,
AC=DC,
∠ACB=∠DCE,
BC=EC,
∴△ABC≌△DEC(SAS)。
SAS
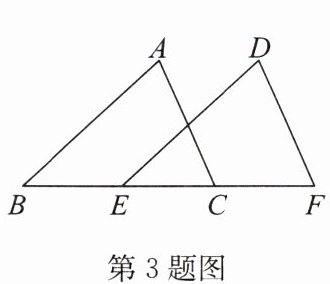
3. 如图,已知AB//DE,AB= DE,需要添加一个条件
BC=EF(或BE=CF)
,就可以根据“SAS”证明△ABC≌△DEF.
答案:BC=EF(或BE=CF)
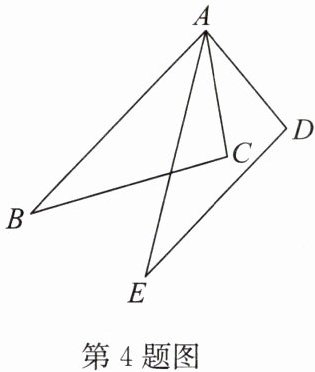
4. (2024·云南)如图,在△ABC和△AED中,AB= AE,∠BAE= ∠CAD,AC= AD.求证:△ABC≌△AED.
答案:证明:
∵∠BAE=∠CAD,
∴∠BAE+∠CAE=∠CAD+∠CAE,
即∠BAC=∠EAD.
在△ABC与△AED中,$\left\{\begin{array}{l} AB=AE,\\ ∠BAC=∠EAD,\\ AC=AD,\end{array}\right. $
∴△ABC≌△AED(SAS).
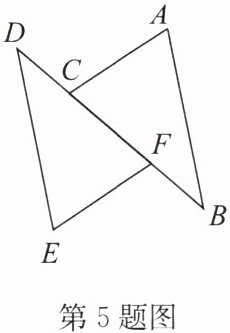
5. 如图,AB//ED,CD= BF,若△ABC≌△EDF,则还需要补充的条件可以是(
C
)
A.AC= EF
B.BC= DF
C.AB= DE
D.∠B= ∠E
答案:C
解析:
证明:
∵AB//ED,
∴∠BAC=∠DEF(两直线平行,内错角相等)。
∵CD=BF,
∴CD+CF=BF+CF,即DF=BC。
若补充条件AB=DE,
在△ABC和△EDF中,
$\left\{\begin{array}{l} AB=DE \\ ∠BAC=∠DEF \\ BC=DF\end{array}\right.$
∴△ABC≌△EDF(SAS)。
C
6. 如图,在△ABC中,AD⊥BC于点D,且BD= CD,则下列结论不成立的是(
D
)
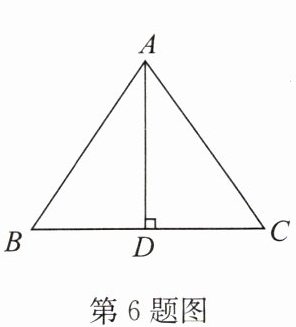
A.∠BAD= ∠CAD
B.∠B= ∠C
C.AB= AC
D.BC= CA
答案:D
解析:
∵AD⊥BC,BD=CD,
∴AD是BC的垂直平分线,
∴AB=AC,∠B=∠C,∠BAD=∠CAD,
故A、B、C成立,D不成立。
答案:D
7. 如图,CA平分∠DCB,CB= CD,DA的延长线交BC于点E.若∠EAC= 50°,则∠BAE的度数为
80°
.
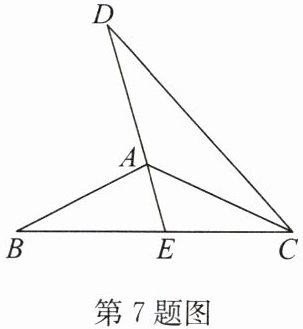
答案:80°
解析:
证明:
∵CA平分∠DCB,
∴∠DCA=∠BCA.
在△DCA和△BCA中,
$\left\{\begin{array}{l} CD=CB\\ ∠DCA=∠BCA\\ CA=CA\end{array}\right.$
∴△DCA≌△BCA(SAS).
∴∠DAC=∠BAC.
∵∠EAC=50°,∠DAC+∠EAC=180°,
∴∠DAC=130°.
∴∠BAC=130°.
∵∠BAE+∠EAC=∠BAC,
∴∠BAE=∠BAC-∠EAC=130°-50°=80°.
80°
8. 如图,点B在AE上,BC= BD,∠CBE= ∠DBE.若∠CAD= 60°,则∠CAE=
30°
.
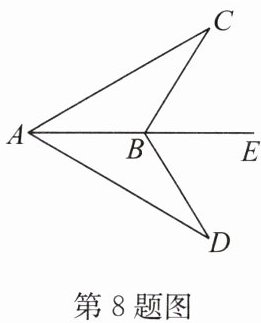
答案:30°
解析:
证明:在△CBE和△DBE中,
$\begin{cases}BC = BD \\\angle CBE = \angle DBE \\BE = BE\end{cases}$
∴△CBE≌△DBE(SAS),
∴∠CEB = ∠DEB,
即AE平分∠CED,
又
∵∠CAD = 60°,
∴∠CAE = $\frac{1}{2}$∠CAD = 30°。
30°