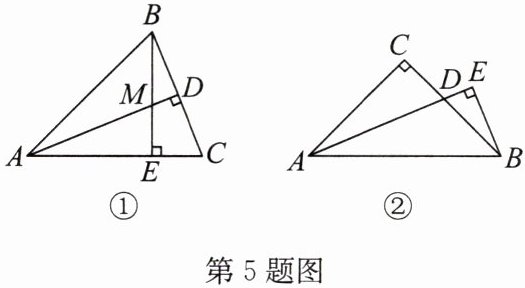
5. (2024·南京鼓楼区期末)(1)如图①,在 $\triangle ABC$ 中,$AB = AC$,$\angle BAC = 45^{\circ}$。$\triangle ABC$ 的高 $AD$ 与高 $BE$ 相交于点 $M$。求证:$AM = 2CD$;
(2)如图②,在 $Rt\triangle ABC$ 中,$\angle C = 90^{\circ}$,$AC = BC$,$AD$ 是 $\angle CAB$ 的平分线,过点 $B$ 作 $BE \perp AD$,交 $AD$ 的延长线于点 $E$。若 $AD = 3$,求 $BE$ 的长。
答案:(1)证明:在△ABC中,∠BAC=45°,BE⊥AC,
∴AE=BE.
∵AD⊥BC,
∴∠EAM=90°-∠C=∠EBC.
在△AEM和△BEC中,$\left\{\begin{array}{l} ∠EAM=∠EBC,\\ AE=BE,\\ ∠AEM=∠BEC,\end{array}\right. $
∴△AEM≌△BEC(ASA).
∴AM=BC.
∵AB=AC,AD⊥BC,
∴BD=CD,
∴BC=2CD,
∴AM=2CD.
(2)解:如答图,延长BE,AC,两线交于点F.
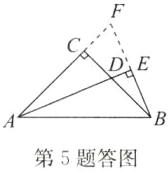
∵BE⊥EA,
∴∠AEF=∠AEB=90°.
∵AD是∠CAB的平分线,
∴∠FAE=∠BAE.
∴∠F=∠ABE,
∴AF=AB.
∵BE⊥EA,
∴BE=EF=$\frac {1}{2}$BF.
在△ABC中,AC=BC,∠ACB=90°,
∴∠CAB=45°.
∴∠AFE=(180°-45°)÷2=67.5°,∠FAE=45°÷2=22.5°.
∴∠CDA=67.5°.
在△ADC和△BFC中,$\left\{\begin{array}{l} ∠ADC=∠F,\\ ∠ACD=∠BCF,\\ AC=BC,\end{array}\right. $
∴△ADC≌△BFC(AAS).
∴BF=AD.
∴BE=$\frac {1}{2}$AD=$\frac {1}{2}$×3=1.5.