1. 如图,在 $\triangle ABC$ 中,$AB = AC$,$D$ 是 $BC$ 的中点,$E$,$F$ 分别是 $AB$,$AC$ 上的点,且 $AE = AF$。求证:$DE = DF$。
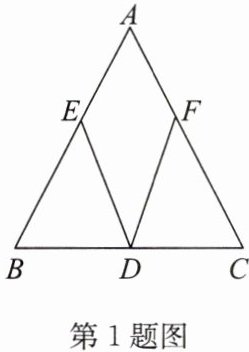
答案:证明:如答图,连接AD.
∵AB=AC,D是BC的中点,
∴∠DAE=∠DAF.
又
∵AE=AF,AD=AD,
∴△ADE≌△ADF(SAS),
∴DE=DF.
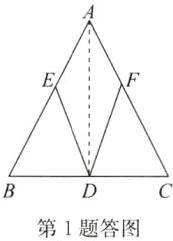
2. (2024·盐城大丰期末)如图,在 $\triangle ABC$ 中,$AB = AC$,$D$ 是 $BC$ 的中点,$P$ 是 $AD$ 上任意一点,$PE \perp AB$ 于点 $E$,$PF \perp AC$ 于点 $F$。
(1)求证:$PE = PF$;
(2)连接 $PB$,$PC$,求证:$PD$ 平分 $\angle BPC$。
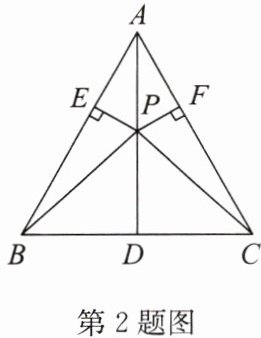
答案:证明:
(1)
∵AB=AC,D是BC的中点,
∴AD平分∠BAC.
又
∵PE⊥AB,PF⊥AC,
∴PE=PF.
(2)
∵AB=AC,D是BC的中点,
∴AD⊥BC,
∴AD垂直平分BC,
∴PB=PC,
∴PD平分∠BPC.
3. (2024·盐城滨海期末)如图,在等边 $\triangle ABC$ 和等边 $\triangle ADE$ 中,$AD$ 是 $BC$ 边上的中线,$DE$ 交 $AC$ 于点 $F$。求证:(1)$AC \perp DE$;(2)$CD = CE$。
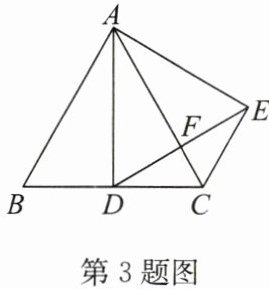
答案:证明:
(1)
∵△ABC是等边三角形,
∴∠BAC=60°,AB=AC.
∵AD是BC边上的中线,
∴AD平分∠BAC,
∴∠DAC=∠BAD=30°.
∵△ADE是等边三角形,
∴∠DAE=60°,AD=AE.
∴∠EAC=30°=∠DAC,
∴AC⊥DE.
(2)
∵AD=AE,AC⊥DE,
∴AC垂直平分DE,
∴CD=CE.