1.【数学探究】
折纸的过程也是开发人类大脑智力以及逻辑思维的一个过程. 数学综合实践课上,老师组织同学们开展了一次折纸探究活动.
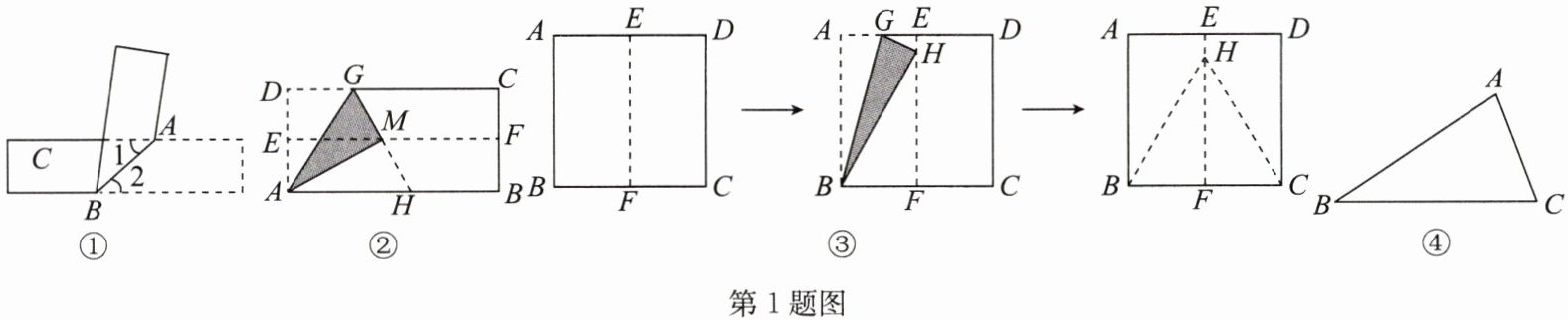
(1)探究一:如图①,在一张长方形纸片上任意画一条线段 $ AB $,将纸片沿 $ AB $ 折叠,重叠的部分 $ \triangle ABC $ 一定是____三角形.
(2)探究二:你能用一张长方形纸片折出一个等边三角形吗?
甲小组使用长方形纸片,操作如下:如图②,把长方形纸片 $ ABCD $ 的宽对折,然后展开,折痕记为 $ EF $;再将点 $ D $ 翻折到 $ EF $ 上的点 $ M $ 处,且使折痕过点 $ A $,折痕与 $ CD $ 的交点为 $ G $;再沿 $ GM $ 折叠,折痕与 $ AB $ 的交点为 $ H $,则 $ \triangle AHG $ 就是一个等边三角形. 请你说明这样做的道理. (说明: $ M $ 是 $ GH $ 的中点,说理时可直接使用)
(3)探究三:你能用一张正方形纸片折出一个等边三角形吗?
乙小组使用正方形纸片,操作如下:如图③,先把正方形纸片 $ ABCD $ 对折后再展开,折痕为 $ EF $;再将点 $ A $ 翻折到 $ EF $ 上的点 $ H $ 处,且使折痕过点 $ B $;最后沿 $ HC $ 折叠,得到的 $ \triangle HBC $ 就是一个等边三角形. 请你说明这样做的道理.
【迁移应用】
折纸也能为数学学习提供解决问题的思路和方法.
如图④,在 $ \triangle ABC $ 中,$ AB>AC $,怎样说明 $ \angle C>\angle B $ 呢? 小亮发现,利用折纸做一个轴对称变化,得到一对全等的三角形,从而可将问题解决.
(4)请画图并说明小亮的解题思路.
答案:(1)等腰
(2)解:在△AMG和△AMH中,AM=AM,∠AMG=∠AMH=90°,MG=MH,所以△AMG≌△AMH(SAS),所以AG=AH,因为∠DAG=∠GAM=∠MAH,所以∠GAH=60°,所以△AHG是一个等边三角形.
(3)解:由折叠得BH=AB=BC,由折叠得EF为BC的垂直平分线,所以HC=BH,所以BH=HC=BC,所以△HBC是等边三角形.
(4)解:思路:如答图,把AC沿∠BAC的平分线AD翻折.
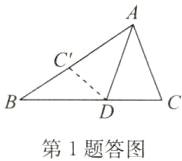
因为AB>AC,所以点C落在AB上的点C'处,即AC=AC',依据以上操作,可得△ACD≌△AC'D,所以∠AC'D=∠C,又因为∠AC'D>∠B,所以∠C>∠B.