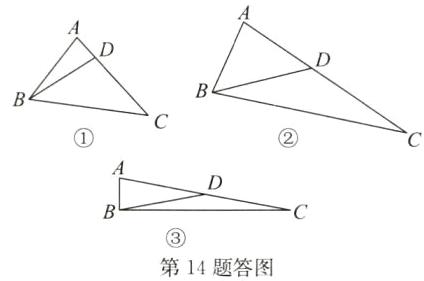
12. (2025·吴江区期末)如图,△ABC 是边长为 10 cm 的等边三角形,动点 P 从点 B 出发以 3 cm/s 的速度沿着路线 B→A→C→B 向终点 B 运动,同时动点 Q 从点 C 出发以 2 cm/s 的速度沿着路线 C→B→A→C 向终点 C 运动,设运动的时间为 t s.
(1)当点 P 在 AB 边上运动时,BP = ______cm,BQ = ______cm;
(2)当△BPQ 是等边三角形时,求 t 的值.
答案:(1)3t 10 - 2t
(2)解:
∵△BPQ是等边三角形,
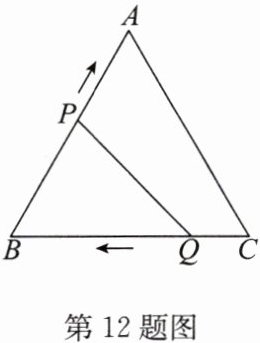
∴BP=BQ. 如答图①,当点P在AB边上时,点Q在BC边上, 则有3t=10 - 2t,解得t=2; 如答图②,当点P在BC边上时,点Q在AB边上, 则有30 - 3t=2t - 10,解得t=8. 综上,当△BPQ是等边三角形时,t=2或8.
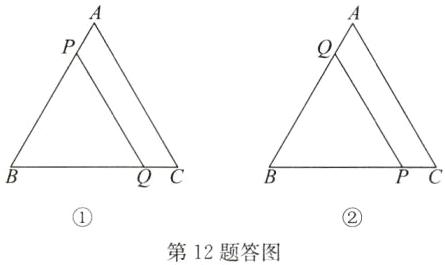
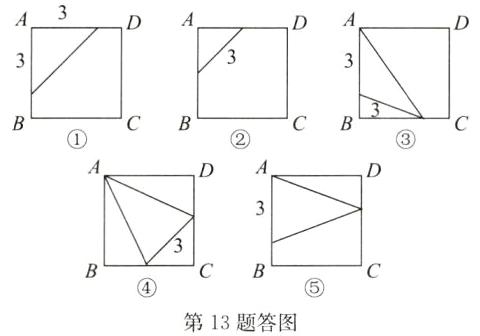
13. 如图,在边长为 4 的正方形 ABCD 中,请画出以点 A 为一个顶点,另外两个顶点在正方形 ABCD 的边上,且一边长为 3 的所有大小不同的等腰三角形. (要求:只画出示意图,并在所画等腰三角形长为 3 的边上标注数字 3)
答案:解:如答图所示.
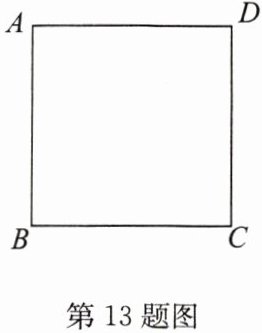
14. 在△ABC 中,∠A = 80°,过△ABC 的顶点 B 的直线将△ABC 分割成两个等腰三角形,求∠C 的度数. (请画图分析)
答案:解:如答图①,
∵AB=BD=CD,∠A=80°,
∴∠ADB=∠A=80°,∠DBC=∠C.
∵∠ADB=∠DBC+∠C,
∴∠C= $\frac{1}{2}$∠ADB=40°. 如答图②,
∵AB=AD,CD=BD,∠A=80°,
∴∠ADB=∠ABD= $\frac{1}{2}$(180° - ∠A)=50°,∠DBC=∠C.
∵∠ADB=∠DBC+∠C,
∴∠C= $\frac{1}{2}$∠ADB=25°. 如答图③,
∵AD=BD=CD,
∴∠A=∠DBA=80°,∠C=∠DBC,
∴∠C= $\frac{180° - 2×80°}{2}$=10°. 综上所述,∠C的度数为40°或25°或10°.