1. 在$\triangle ABC$中,$AB = AC$,$\angle B = 70^{\circ}$,则$\angle A = $(
B
)
A.$70^{\circ}$
B.$40^{\circ}$
C.$60^{\circ}$
D.$80^{\circ}$
答案:B
解析:
在$\triangle ABC$中,$AB=AC$,故$\triangle ABC$为等腰三角形,所以$\angle B=\angle C$。已知$\angle B=70^{\circ}$,则$\angle C=70^{\circ}$。因为三角形内角和为$180^{\circ}$,所以$\angle A=180^{\circ}-\angle B-\angle C=180^{\circ}-70^{\circ}-70^{\circ}=40^{\circ}$。
B
2. (2024·宿豫期末)如图,在$\triangle ABC$中,$AB = AC$,$AD\perp BC$,垂足为$D$。若$\angle B = 43^{\circ}$,则$\angle CAD$的度数为
47°
。
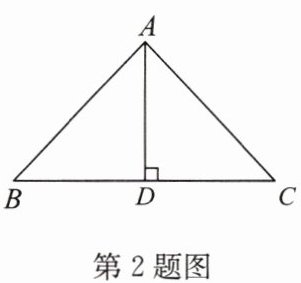
答案:47°
解析:
解:在$\triangle ABC$中,$AB=AC$,故$\triangle ABC$为等腰三角形,$\angle B=\angle C=43^{\circ}$。
因为$AD\perp BC$,所以$\angle ADC=90^{\circ}$。
在$\triangle ADC$中,$\angle CAD=180^{\circ}-\angle ADC-\angle C=180^{\circ}-90^{\circ}-43^{\circ}=47^{\circ}$。
$47^{\circ}$
3. (2024·绥化)如图,$AB// CD$,$\angle C = 33^{\circ}$,$OC = OE$,则$\angle A = $
66
$^{\circ}$。
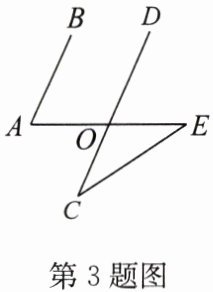
答案:66
解析:
解:
∵ $OC = OE$,
∴ $\angle E = \angle C = 33°$。
∵ $\angle AOD$ 是 $\triangle COE$ 的外角,
∴ $\angle AOD = \angle C + \angle E = 33° + 33° = 66°$。
∵ $AB // CD$,
∴ $\angle A = \angle AOD = 66°$。
$66$
4. 一个等腰三角形的两边长分别为$4\ cm和8\ cm$,则其周长是
20
$cm$。
答案:20
解析:
情况一:腰长为$4\ cm$,底边长为$8\ cm$。
$4 + 4 = 8$,不满足三角形两边之和大于第三边,舍去。
情况二:腰长为$8\ cm$,底边长为$4\ cm$。
$8 + 4 > 8$,$8 + 8 > 4$,满足三角形三边关系。
周长为$8 + 8 + 4 = 20\ cm$。
20
5. 如图,$BE是\triangle ABC$的角平分线,在$AB上取点D$,使$DB = DE$。
(1)求证:$DE// BC$;
(2)若$\angle A = 65^{\circ}$,$\angle AED = 45^{\circ}$,求$\angle EBC$的度数。
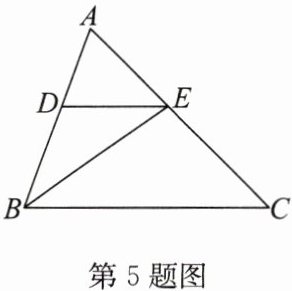
答案:
(1)证明:
∵BE是△ABC的角平分线,
∴∠DBE=∠EBC.
∵DB=DE,
∴∠DEB=∠DBE,
∴∠DEB=∠EBC,
∴DE//BC;
(2)解:
∵DE//BC,
∴∠C=∠AED=45°.在△ABC中,∠A+∠ABC+∠C=180°,
∴∠ABC=180°-∠A-∠C=180°-65°-45°=70°.
∵BE是△ABC的角平分线,
∴∠EBC=$\frac{1}{2}$∠ABC=35°.
6. 如图,直线$a// b$,直线$l与直线a$,$b分别相交于点A$,$B$,点$C在直线b$上,且$CA = CB$。若$\angle 1 = 32^{\circ}$,则$\angle 2$的度数为(
C
)
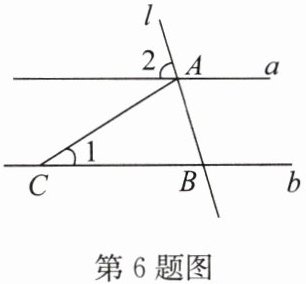
A.$32^{\circ}$
B.$58^{\circ}$
C.$74^{\circ}$
D.$75^{\circ}$
答案:C
7. 如图,在四边形$ABCD$中,点$E在边AD$上,$\angle BCE = \angle ACD$,$\angle BAC = \angle D = 40^{\circ}$,$AB = DE$,$AC = AE$,则$\angle B$的度数为(
C
)
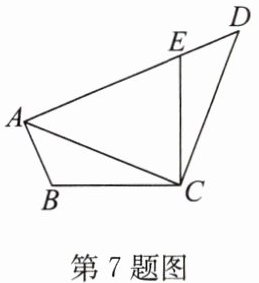
A.$105^{\circ}$
B.$115^{\circ}$
C.$110^{\circ}$
D.$120^{\circ}$
答案:C
解析:
证明:
∵∠BCE=∠ACD,
∴∠BCE-∠ACE=∠ACD-∠ACE,即∠BCA=∠ECD.
∵AC=AE,∠BAC=40°,
∴∠AEC=∠ACE=(180°-40°)/2=70°,
∴∠DEC=180°-∠AEC=110°.
在△ABC和△EDC中,
∵AB=DE,∠BAC=∠D=40°,∠BCA=∠ECD,
∴△ABC≌△EDC(ASA),
∴∠B=∠DEC=110°.
110°
8. (2024·内江)如图,在$\triangle ABC$中,$\angle DCE = 40^{\circ}$,$AE = AC$,$BC = BD$,则$\angle ACB$的度数为
100°
。
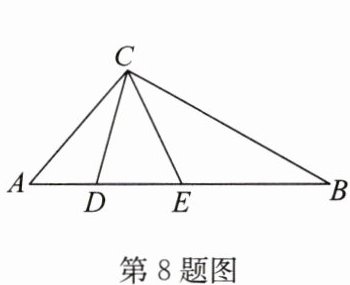
答案:100°
解析:
证明:设$\angle ACB = x$,则$\angle ACD+\angle BCE=x-40°$。
因为$AE = AC$,所以$\angle AEC=\angle ACE=\angle ACD + 40°$,故$\angle A=180°-2\angle AEC=180°-2(\angle ACD + 40°)=100°-2\angle ACD$。
因为$BC = BD$,所以$\angle BDC=\angle BCD=\angle BCE + 40°$,故$\angle B=180°-2\angle BDC=180°-2(\angle BCE + 40°)=100°-2\angle BCE$。
在$\triangle ABC$中,$\angle A+\angle B+\angle ACB=180°$,即:
$\begin{aligned}(100°-2\angle ACD)+(100°-2\angle BCE)+x&=180°\\200°-2(\angle ACD+\angle BCE)+x&=180°\\200°-2(x - 40°)+x&=180°\\200°-2x + 80°+x&=180°\\280°-x&=180°\\x&=100°\end{aligned}$
$\angle ACB=100°$
100°