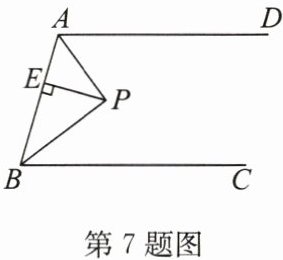
7. 如图,AD//BC,∠ABC 的平分线与∠BAD 的平分线相交于点 P,PE⊥AB,垂足为 E,PE = 5,则 AD 与 BC 之间的距离为
10
.
答案:10
解析:
证明:过点 $ P $ 作 $ PF \perp AD $ 于点 $ F $,$ PG \perp BC $ 于点 $ G $。
∵ $ AP $ 平分 $ \angle BAD $,$ PE \perp AB $,$ PF \perp AD $,
∴ $ PF = PE = 5 $。
∵ $ BP $ 平分 $ \angle ABC $,$ PE \perp AB $,$ PG \perp BC $,
∴ $ PG = PE = 5 $。
∵ $ AD // BC $,
∴ $ AD $ 与 $ BC $ 之间的距离为 $ PF + PG = 5 + 5 = 10 $。
10
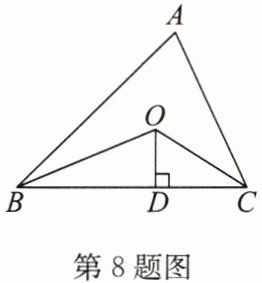
8. (2024·宿城期中)如图,已知△ABC 的周长是 22,BO,CO 分别平分∠ABC 和∠ACB,OD⊥BC 于点 D,且 OD = 3,则△ABC 的面积是
33
.
答案:33
解析:
证明:连接AO,过点O作OE⊥AB于点E,OF⊥AC于点F。
∵BO平分∠ABC,OD⊥BC,OE⊥AB,
∴OE=OD=3。
同理,OF=OD=3。
∵△ABC的周长是22,
∴AB+BC+AC=22。
∴S△ABC=S△ABO+S△BCO+S△ACO
=$\frac{1}{2}$AB·OE+$\frac{1}{2}$BC·OD+$\frac{1}{2}$AC·OF
=$\frac{1}{2}$×3×(AB+BC+AC)
=$\frac{1}{2}$×3×22
=33。
33
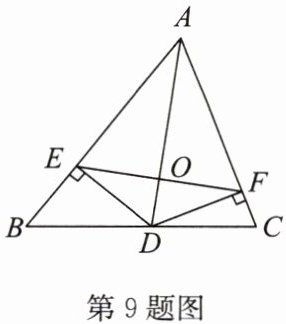
9. 如图,AD 是△ABC 的角平分线,DE,DF 分别是△ABD 和△ACD 的高.
(1)试说明 AD 垂直平分 EF;
(2)若 AB = 8,AC = 6,$S_{△ABC}$ = 28,求 DE 的长.
答案:解:
(1)
∵DE,DF分别是△ABD和△ACD的高,
∴∠AED=∠AFD=90°,即DE⊥AB,DF⊥AC.
∵AD是△ABC的角平分线,
∴∠DAE=∠DAF,从而∠ADE=∠ADF;
又
∵DE⊥AB,DF⊥AC,
∴AE=AF,DE=DF,
∴点A,D均在线段EF的垂直平分线上,
∴AD垂直平分EF.
(2)
∵S△ABC=S△ABD+S△ACD=28,AB=8,AC=6,
∴$\frac{1}{2}AB\cdot DE+\frac{1}{2}AC\cdot DF=28$,
即$\frac{1}{2}×8× DE+\frac{1}{2}×6\cdot DE=28$,
∴DE=4.
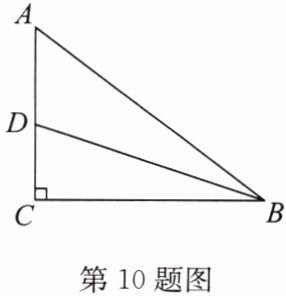
10. (2024·宿城期中)如图,△ABC 是直角三角形,∠C = 90°,点 D 在边 AC 上,连接 BD.
(1)在边 BC 上作点 E,使得点 E 到 BD 的距离与 CE 的长相等(要求:仅用尺规作图,不写作法,保留作图痕迹);
(2)在(1)的条件下继续探究,若 AE = BE,BD = 11,AD = 4,求 CD 的长.
答案:解:
(1)如答图,点E即为所作.
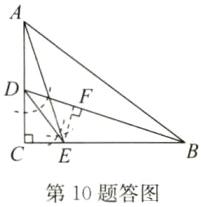
(2)如答图,过点E作EF⊥BD于点F,由作图知DE 平分∠BDC,
∴∠CDE=∠FDE.
又
∵∠C=∠DFE=90°,DE=DE,
∴△CDE≌△FDE(AAS),
∴DC=DF,CE=FE.
又
∵AE=BE,
∴Rt△ACE≌Rt△BFE(HL).
∴BF=AC.
∵BD=11,AD=4,
∴AD+2CD=11,
即4+2CD=11,
∴CD=3.5.