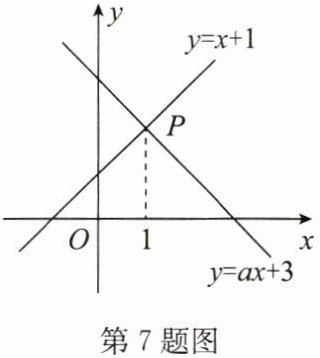
7. (2024·宿迁共同体期末)如图,已知函数 $y = x + 1$ 和 $y = ax + 3$ 的图象交于点 $P$,点 $P$ 的横坐标为 $1$,则关于 $x$,$y$ 的方程组 $\begin{cases}x - y = -1, \\ ax - y = -3\end{cases} $ 的解是
$\left\{\begin{array}{l} x=1\\ y=2\end{array}\right. $
.
答案:$\left\{\begin{array}{l} x=1\\ y=2\end{array}\right. $
解析:
解:因为点$P$是函数$y = x + 1$和$y = ax + 3$的交点,且点$P$的横坐标为$1$,
将$x = 1$代入$y = x + 1$,得$y = 1 + 1 = 2$,所以点$P$的坐标为$(1, 2)$。
又因为方程组$\begin{cases}x - y = -1 \\ ax - y = -3\end{cases}$可变形为$\begin{cases}y = x + 1 \\ y = ax + 3\end{cases}$,
所以方程组的解即为两函数图象交点的坐标,
故方程组的解是$\begin{cases}x = 1 \\ y = 2\end{cases}$。
$\begin{cases}x=1\\ y=2\end{cases}$
8. (2024·泰州一模)若一次函数 $y = x + 1$ 与 $y = -x - 1$ 的图象交于 $A$ 点,则 $A$ 点的坐标为
(-1,0)
.
答案:(-1,0)
解析:
联立方程组:
$\begin{cases}y = x + 1 \\y = -x - 1\end{cases}$
将$y = x + 1$代入$y = -x - 1$,得:
$x + 1 = -x - 1$
移项得:$x + x = -1 - 1$
合并同类项得:$2x = -2$
解得:$x = -1$
将$x = -1$代入$y = x + 1$,得$y = -1 + 1 = 0$
所以$A$点的坐标为$(-1, 0)$
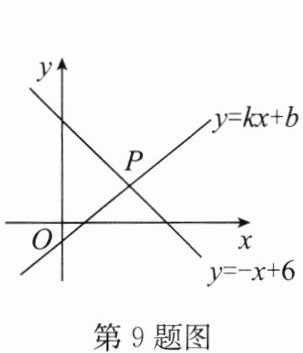
9. (2024·宿城期末)如图,一次函数 $y = kx + b$ 与 $y = -x + 6$ 的图象相交于点 $P$.若点 $P$ 的纵坐标为 $2$,则关于 $x$,$y$ 的二元一次方程组 $\begin{cases}y = kx + b, \\ y = -x + 6\end{cases} $ 的解为
$\left\{\begin{array}{l} x=4\\ y=2\end{array}\right. $
.
答案:$\left\{\begin{array}{l} x=4\\ y=2\end{array}\right. $
解析:
解:因为点 $ P $ 是一次函数 $ y = kx + b $ 与 $ y = -x + 6 $ 的交点,且点 $ P $ 的纵坐标为 $ 2 $,
所以将 $ y = 2 $ 代入 $ y = -x + 6 $,得:
$ 2 = -x + 6 $
解得 $ x = 4 $
所以点 $ P $ 的坐标为 $ (4, 2) $
因此,二元一次方程组 $ \begin{cases} y = kx + b \\ y = -x + 6 \end{cases} $ 的解为 $ \begin{cases} x = 4 \\ y = 2 \end{cases} $
$\begin{cases} x=4 \\ y=2 \end{cases}$
10. 已知三条直线:$(m - 2)x - y = 1$,$x - y = 3$,$2x - y = 2$ 相交于同一点,则 $m = $
5
.
答案:5
解析:
联立方程$\begin{cases}x - y = 3 \\ 2x - y = 2\end{cases}$,
用第二个方程减第一个方程得:$2x - y - (x - y) = 2 - 3$,
即$x = -1$,
将$x = -1$代入$x - y = 3$,得$-1 - y = 3$,解得$y = -4$,
所以交点坐标为$(-1, -4)$,
把$(-1, -4)$代入$(m - 2)x - y = 1$,得$(m - 2)(-1) - (-4) = 1$,
即$-m + 2 + 4 = 1$,$-m + 6 = 1$,$-m = -5$,解得$m = 5$。
5
11. 在平面直角坐标系 $xOy$ 中,点 $P$ 的坐标为 $(m + 1,m - 1)$.
(1)试判断点 $P$ 是否在一次函数 $y = x - 2$ 的图象上,并说明理由;
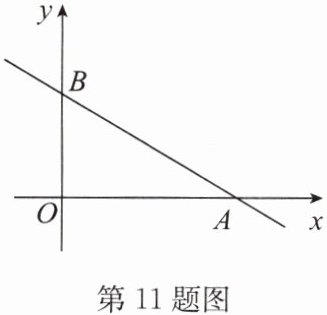
(2)如图,一次函数 $y = -\frac{1}{2}x + 3$ 的图象与 $x$ 轴、$y$ 轴分别相交于点 $A$,$B$,若点 $P$ 在 $\triangle AOB$ 的内部,求 $m$ 的取值范围.
答案:解:
(1)点P在一次函数y=x-2的图象上.理由如下:当x=m+1时,y=m+1-2=m-1,
∴点P(m+1,m−1)在一次函数y=x-2的图象上.
(2)
∵函数$y=-\frac{1}{2}x+3$,
∴A(6,0),B(0,3).
∵点P在△AOB的内部,
∴$0<m+1<6,0<m−1<3,m−1<-\frac{1}{2}(m+1)+3$,
∴$1<m<\frac{7}{3}$.
12. 点 $P(x,y)$ 在第一象限,且 $x + y = 8$,点 $A$ 的坐标为 $(6,0)$.设 $\triangle OPA$ 的面积为 $S$.
(1)用含 $x$ 的式子表示 $S$,写出 $x$ 的取值范围;
(2)当 $\triangle OPA$ 的面积为 $15$ 时,求点 $P$ 的坐标;
(3)$\triangle OPA$ 的面积能大于 $24$ 吗?请说明理由.
答案:解:
(1)
∵点A和点P的坐标分别是(6,0),(x,y),
∴$S=\frac{1}{2}OA\cdot |y_{P}|=\frac{1}{2}×6×|y|=3y$.
∵x+y=8,
∴y=8-x.
∴S=3(8-x)=24-3x.
∵S=-3x+24>0,解得x<8.
又
∵点P在第一象限,
∴x>0,
∴x的取值范围为0<x<8.
(2)当△OPA的面积为15时,24-3x=15,解得x=3,
∴y=8-3=5,
∴点P的坐标为(3,5).
(3)不能.理由如下:
假设△OPA的面积大于24,
则-3x+24>24,解得x<0,
∵0<x<8,
∴△OPA的面积不能大于24.