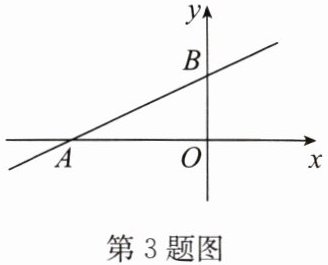
3. (2024·扬州)如图,已知一次函数 $y = kx + b(k \neq 0)$ 的图象分别与 $x$ 轴、$y$ 轴交于 $A$,$B$ 两点,若 $OA = 2$,$OB = 1$,则关于 $x$ 的方程 $kx + b = 0$ 的解为
x=-2
.
解析:
解:
∵一次函数$y = kx + b(k \neq 0)$的图象与$x$轴交于点$A$,$OA = 2$,
∴点$A$的坐标为$(-2, 0)$或$(2, 0)$。
又
∵函数图象与$y$轴交于点$B$,$OB = 1$,结合图象可知点$B$在$y$轴正半轴,即$b>0$,且函数图象从左到右上升,$k>0$,此时点$A$在$x$轴负半轴,
∴点$A$的坐标为$(-2, 0)$。
∵关于$x$的方程$kx + b = 0$的解为一次函数$y = kx + b$的图象与$x$轴交点的横坐标,
∴方程$kx + b = 0$的解为$x=-2$。
$x=-2$