1. 在平面直角坐标系中,一次函数 $ y = 2x - 3 $ 的大致图象是(
D
)
]
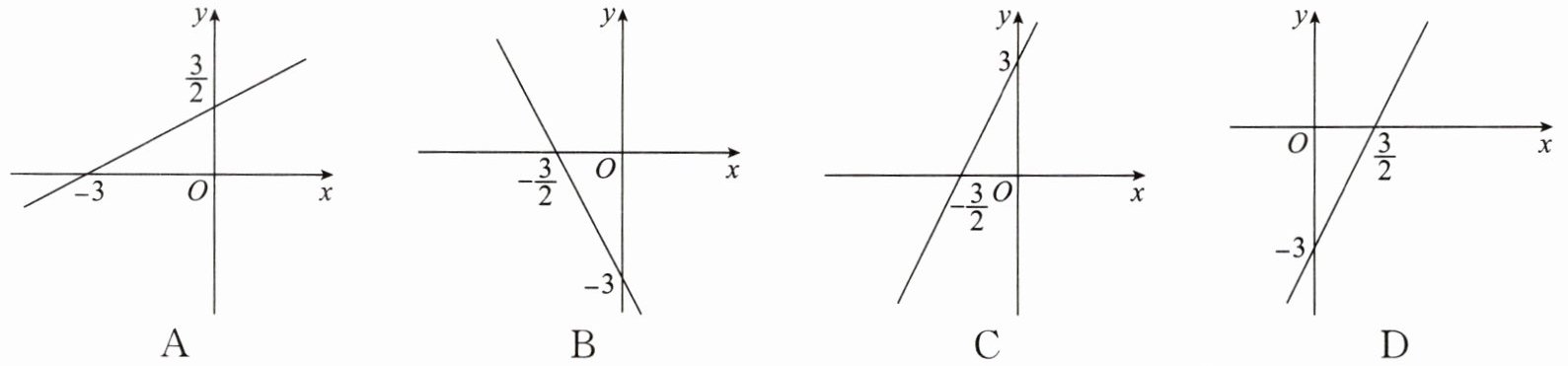
答案:D
解析:
解:对于一次函数 $ y = 2x - 3 $,
因为斜率 $ 2 > 0 $,所以函数图象从左到右上升。
当 $ x = 0 $ 时,$ y = -3 $,即与 $ y $ 轴交于点 $ (0, -3) $。
当 $ y = 0 $ 时,$ 2x - 3 = 0 $,解得 $ x = \frac{3}{2} $,即与 $ x $ 轴交于点 $ \left( \frac{3}{2}, 0 \right) $。
综上,符合条件的图象是 D。
D
2. (2024·宿城期末)若一次函数 $ y = kx + 4 $ 的图象经过点 $ (2, - 4) $,则 $ k $ 的值为
-4
。
答案:-4
解析:
将点$(2, -4)$代入$y = kx + 4$,得$-4 = 2k + 4$,解得$k = -4$。
$-4$
3. (2024·天津改编)若一次函数 $ y = kx + 3 $($ k $ 是常数,$ k \neq 0 $)的图象经过第一、三象限,则 $ k $ 的值可以是
1(答案不唯一)
(写出一个即可)。
答案:1(答案不唯一)
4. 将正比例函数 $ y = - 3x $ 的图象向上平移 $ 5 $ 个单位长度,得到的图象的函数表达式为
$y = -3x + 5$
。
答案:$y = -3x + 5$
5. 画出下列函数的图象。
(1) $ y = 2x - 1 $;
(2) $ y = - \frac{1}{2}x + 1 $。
答案:解:
(1)列表如下.
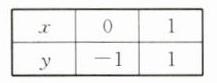
描点:函数图象过两点$(0, -1),(1, 1)$;
画线:过两点画直线,如答图①.
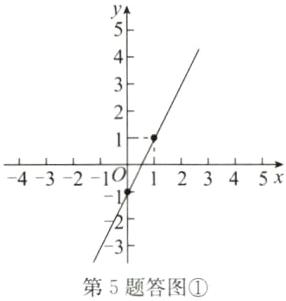
(2)列表如下.
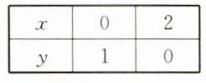
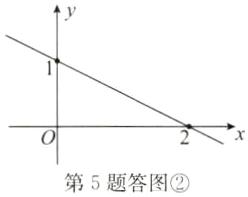
描点、画线,其图象如答图②.
6. (2024·宿城期末)已知点 $ P(m, n) $ 在第三象限,则函数 $ y = nx + m $ 的图象大致是(
B
)
]
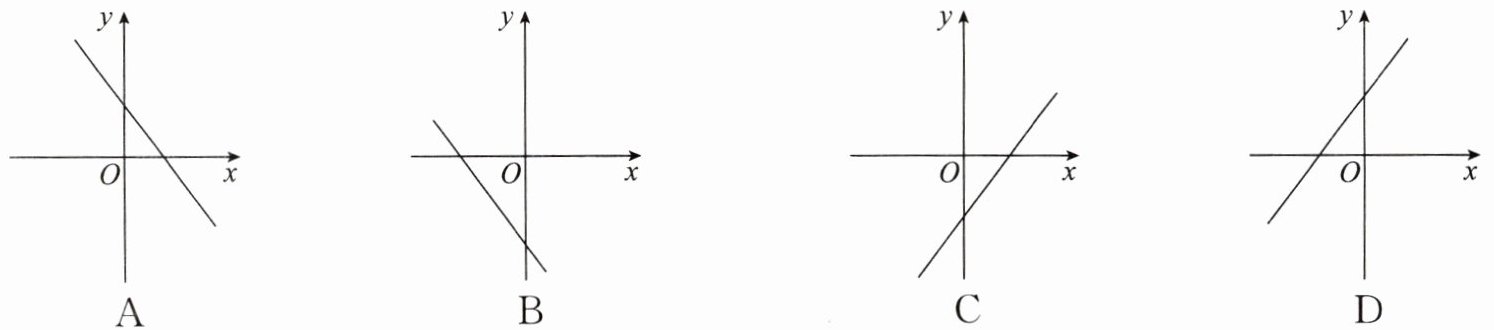
答案:B
解析:
解:
∵点$P(m,n)$在第三象限,
∴$m<0$,$n<0$。
∵函数$y=nx+m$中,$n<0$,$m<0$,
∴函数$y=nx+m$的图象经过第二、三、四象限。
答案:B
7. 已知 $ A $ 是直线 $ y = x + 1 $ 上一点,其横坐标为 $ - 3 $,若点 $ B $ 与点 $ A $ 关于 $ y $ 轴对称,则点 $ B $ 的坐标为
$(3, -2)$
。
答案:$(3, -2)$
解析:
当$x = -3$时,$y=-3 + 1=-2$,则点$A$的坐标为$(-3,-2)$。
因为点$B$与点$A$关于$y$轴对称,所以点$B$的横坐标为$3$,纵坐标为$-2$,即点$B$的坐标为$(3,-2)$。
$(3,-2)$
8. 已知一次函数 $ y = kx + b $ 的图象经过点 $ (1, 3) $ 和 $ ( - 1, 2) $,则 $ k^{2} - b^{2} = $
-6
。
答案:-6
解析:
解:将点$(1, 3)$和$(-1, 2)$代入$y = kx + b$,得
$\begin{cases}k + b = 3 \\-k + b = 2\end{cases}$
解得$k = \frac{1}{2}$,$b = \frac{5}{2}$。
$k^2 - b^2=(k + b)(k - b)=3×\left(\frac{1}{2}-\frac{5}{2}\right)=3×(-2)=-6$
-6
9. 在一次函数 $ y = x + 3 $ 的图象上,到 $ y $ 轴的距离等于 $ 2 $ 的点的坐标是
$(2, 5)$或$(-2, 1)$
。
答案:$(2, 5)$或$(-2, 1)$
解析:
到$y$轴的距离等于$2$的点,其横坐标为$2$或$-2$。
当$x = 2$时,$y=2 + 3=5$,点的坐标为$(2,5)$;
当$x=-2$时,$y=-2 + 3=1$,点的坐标为$(-2,1)$。
$(2, 5)$或$(-2, 1)$