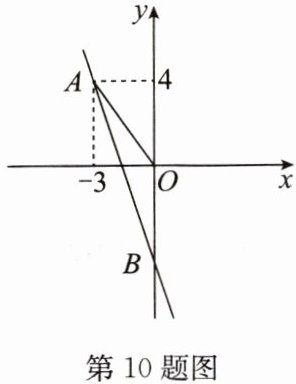
10. 如图,点 $ A( - 3, 4) $ 在一次函数 $ y = - 3x + b $ 的图象上,该一次函数的图象与 $ y $ 轴的交点为 $ B $,那么 $ \triangle AOB $ 的面积为
$\frac{15}{2}$
。
答案：$\frac{15}{2}$
解析：
解：因为点$ A(-3, 4) $在一次函数$ y = -3x + b $的图象上，所以将$ x=-3 $，$ y=4 $代入函数得：$ 4 = -3×(-3) + b $，即$ 4 = 9 + b $，解得$ b = -5 $。所以该一次函数解析式为$ y = -3x - 5 $。
令$ x = 0 $，则$ y = -5 $，所以点$ B $的坐标为$ (0, -5) $，则$ OB = |-5| = 5 $。
点$ A $到$ y $轴的距离为点$ A $横坐标的绝对值，即$ |-3| = 3 $。
所以$ \triangle AOB $的面积为$ \frac{1}{2} × OB × 3 = \frac{1}{2} × 5 × 3 = \frac{15}{2} $。
$\frac{15}{2}$
11. 若三点 $ (1, 4) $,$ (2, 7) $,$ (a, 10) $ 在同一条直线上,求 $ a $ 的值。
答案：解:设经过$(1, 4),(2, 7)$两点的直线的函数表达式为$y = kx + b$.$\therefore \left\{\begin{array}{l} k + b = 4\\ 2k + b = 7\end{array}\right.,\therefore \left\{\begin{array}{l} k = 3\\ b = 1\end{array}\right.,\therefore y = 3x + 1$,将$(a, 10)$代入函数表达式,得$3a + 1 = 10,\therefore a = 3$.
12. 已知三点 $ A(1, 0) $,$ B(0, 4) $,$ C(4, 2) $。
(1) 在如图所示的平面直角坐标系中画出 $ \triangle ABC $；
(2) 若 $ C $ 点与 $ C' $ 点关于 $ x $ 轴对称,求直线 $ BC' $ 的函数表达式。
答案：解:
(1)在$y = 2x + 8$中,当$x = -2$时,$y = 2×(-2) + 8 = 4$,从而$P(-2, 4)$.
∵直线$l_{1}:y = kx + 2$过点$P$,$\therefore 4 = -2k + 2$,解得$k = -1$.
∴直线$l_{1}$的函数表达式为$y = -x + 2$.
(2)
∵直线$l_{1}:y = -x + 2$交$x$轴于点$B(2, 0)$,交$y$轴于点$C(0, 2)$,直线$y = 2x + 8$交$x$轴于点$A(-4, 0)$,$\therefore AB = 6$,$OB = 2 = OC$.
$\therefore S_{四边形OAPC}=S_{\triangle PAB}-S_{\triangle BOC}=\frac{1}{2}AB\cdot|y_{P}|-\frac{1}{2}OB\cdot OC=\frac{1}{2}×6×4-\frac{1}{2}×2×2 = 10$.
13. (2024·湖滨新区期末)如图,已知直线 $ l_{1}:y = kx + 2 $ 与 $ x $ 轴交于点 $ B $,与 $ y $ 轴交于点 $ C $,与直线 $ l_{2}:y = 2x + 8 $ 交于点 $ P( - 2, a) $,直线 $ l_{2} $ 与 $ x $ 轴交于点 $ A $。
(1) 求直线 $ l_{1} $ 的函数表达式；
(2) 求四边形 $ OAPC $ 的面积。
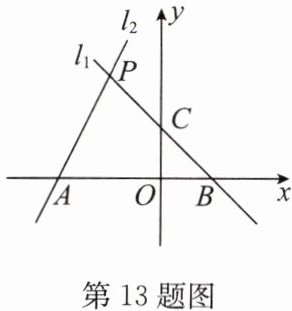
答案：解：(1)在$y = 2x + 8$中，当$x = - 2$时，$y = 2×(-2)+8 = 4$，所以$P(-2,4)$。
$\because$直线$l_{1}:y = kx + 2$过点$P$，$\therefore4 = - 2k + 2$，解得$k = - 1$。
$\therefore$直线$l_{1}$的函数表达式为$y = - x + 2$。
(2)$\because$直线$l_{1}:y = - x + 2$交$x$轴于点$B(2,0)$，交$y$轴于点$C(0,2)$，直线$y = 2x + 8$交$x$轴于点$A(-4,0)$，
$\therefore AB = 6$，$OB = 2 = OC$。
$\because S_{\triangle ABC}=\frac{1}{2}AB\cdot|y_{C}|=\frac{1}{2}OB\cdot OC$，
$\therefore\frac{1}{2}×6×2=\frac{1}{2}×2×2 + 10$。
