答案：解:
(1)由题意,得$\begin{cases} 2m+1 \neq 0,\\ m-3=0,\\ \end{cases}$解得$m=3$,
$\therefore$该函数表达式为$y=7x$.
(2)$y_{1} ＞ y_{2}$.

答案：
解:
(1)如答图,设$A(3,m)$,由$AH \perp x$轴于点$H$,$\triangle AOH$的面积为3,得$OH=3$,$AH=-m$,且$\dfrac{1}{2}×3×(-m)=3$,解得$m=-2$,故$A(3,-2)$.
$\because$正比例函数$y=kx$的图象经过点$A$,
$\therefore 3k=-2$,解得$k=-\dfrac{2}{3}$.
$\therefore$正比例函数的表达式为$y=-\dfrac{2}{3}x$.

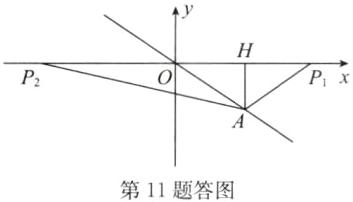
(2)存在.如答图,设$P(t,0)$,则$OP=|t|$,由$\triangle AOP$的面积是$\triangle AOH$的面积的2倍,得$OP=2OH=6$,
$\therefore |t|=6$,解得$t= \pm 6$.
$\therefore$存在满足条件的点$P$,其坐标为$(-6,0)$和$(6,0)$.

答案：
解:
(1)$\because$直线$y=kx(k \neq 0)$经过点$A(1,-3)$,
$\therefore 1× k=-3$,$\therefore k=-3$.
$\therefore$直线$OA$的函数表达式为$y=-3x$.
(2)如答图,过点$A$作$AC \perp x$轴于点$C$,则$AC=3$.
由$\angle OBA=60^{ \circ }$,得$\angle BAC=30^{ \circ }$,
$\therefore BC=\dfrac{1}{2}AB$.
在$Rt \triangle ABC$中,由勾股定理,得$AC^{2}+BC^{2}=AB^{2}$,
$\therefore 3^{2}+\left(\dfrac{1}{2}AB\right)^{2}=AB^{2}$,解得$AB=2\sqrt{3}$.
$\therefore$线段$AB$的长为$2\sqrt{3}$.