7. 已知在6件产品中,有2件次品,任取2件产品都是次品的概率是(
D
)
A.$\frac{1}{5}$
B.$\frac{1}{6}$
C.$\frac{1}{10}$
D.$\frac{1}{15}$
答案:D
解析:
本题可先求出从$6$件产品中任取$2$件的所有可能情况数,再求出取到的$2$件都是次品的情况数,最后根据古典概型概率公式计算概率。
步骤一:计算从$6$件产品中任取$2$件的所有可能情况数
从$n$个不同元素中取出$m$个元素的组合数记为$C_{n}^m$,其计算公式为$C_{n}^m=\frac{n!}{m!(n - m)!}$。
从$6$件产品中任取$2$件,即$n = 6$,$m = 2$,则所有可能的情况数为:
$C_{6}^2=\frac{6!}{2!(6 - 2)!}=\frac{6×5}{2×1}=15$(种)
步骤二:计算取到的$2$件都是次品的情况数
已知有$2$件次品,从$2$件次品中任取$2$件,即$n = 2$,$m = 2$,则取到的$2$件都是次品的情况数为:
$C_{2}^2=\frac{2!}{2!(2 - 2)!}=1$(种)
步骤三:根据古典概型概率公式计算概率
古典概型概率公式为$P(A)=\frac{事件A包含的基本事件数}{试验的基本事件总数}$。
设“任取$2$件产品都是次品”为事件$A$,由上述计算可知事件$A$包含的基本事件数为$1$,试验的基本事件总数为$15$,则$P(A)=\frac{1}{15}$。
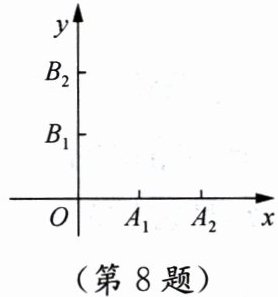
8. 如图,在平面直角坐标系中,点$A_{1}$、$A_{2}在x$轴上,点$B_{1}$、$B_{2}在y$轴上,其坐标分别为$A_{1}(1,0)$、$A_{2}(2,0)$、$B_{1}(0,1)$、$B_{2}(0,2)$,分别以$A_{1}$、$A_{2}$、$B_{1}$、$B_{2}中的任意两点与O$为顶点作三角形,所作的三角形有两条边相等的概率是(
D
)
A.$\frac{3}{4}$
B.$\frac{1}{3}$
C.$\frac{2}{3}$
D.$\frac{1}{2}$
答案:D
解析:
从A₁、A₂、B₁、B₂中任取两点与O构成三角形,需排除三点共线情况。共6种取两点组合:(A₁,A₂)、(A₁,B₁)、(A₁,B₂)、(A₂,B₁)、(A₂,B₂)、(B₁,B₂)。其中(A₁,A₂)、(B₁,B₂)与O共线,不能构成三角形,剩余4个三角形:△OA₁B₁、△OA₁B₂、△OA₂B₁、△OA₂B₂。
△OA₁B₁:OA₁=1,OB₁=1,A₁B₁=√2,有两边相等;
△OA₁B₂:OA₁=1,OB₂=2,A₁B₂=√5,无两边相等;
△OA₂B₁:OA₂=2,OB₁=1,A₂B₁=√5,无两边相等;
△OA₂B₂:OA₂=2,OB₂=2,A₂B₂=2√2,有两边相等。
有两条边相等的三角形共2个,总三角形4个,概率为2/4=1/2。
9. 如图,每一个标有数字的方块均是可以翻动的木牌,其中只有两块木牌的背面贴有中奖标志,任意翻动一块木牌,中奖的概率为
$\frac{1}{3}$
.

答案:$\frac{1}{3}$
解析:
总共有6块木牌,其中2块木牌的背面贴有中奖标志。
根据概率公式,中奖概率为中奖的木牌数除以总木牌数,即:
$P(中奖) = \frac{2}{6} = \frac{1}{3}$。
10. 某校九年级(1)班有男生20人,女生24人,其中男生有18人住宿,女生有20人住宿. 现随机抽一名学生,则抽到一名走读女生的概率是
$\frac{1}{11}$
.
答案:$\frac{1}{11}$(或填$\frac{4}{44}$化简前形式,但通常选择最简形式$\frac{1}{11}$)
解析:
该班总人数为:$20 + 24 = 44$(人),
走读女生人数为:$24 - 20 = 4$(人),
所以,抽到一名走读女生的概率为:$P = \frac{4}{44} = \frac{1}{11}$。
11. 从0至9这10个自然数中,任取1个数,这个数小于5的概率是
1/2
.
答案:1/2
解析:
从0至9这10个自然数中,小于5的数有0、1、2、3、4,共5个。任取1个数,总共有10种等可能的结果,其中符合条件的结果有5种,所以概率为5÷10=1/2。
12. 小明连续抛掷5次质地均匀的骰子都没有得到点数6,则他第6次抛掷得到点数6的概率是
$\frac{1}{6}$
.
答案:$\frac{1}{6}$
解析:
抛掷质地均匀的骰子,每次出现点数6的概率均为独立事件,不受之前抛掷结果影响,故第6次抛掷得到点数6的概率是$\frac{1}{6}$。
13. 如图,4张卡片上分别写有$-2$、$\sqrt{3}$、$\frac{5}{7}$、$\pi$,从中任取2张卡片,2张卡片都写有无理数的概率是
$\frac{1}{6}$
.

答案:$\frac{1}{6}$
解析:
本题可先确定从四张卡片中任取$2$张卡片的所有可能情况,再找出$2$张卡片都写有无理数的情况,最后根据古典概型概率公式计算概率。
步骤一:计算从四张卡片中任取$2$张卡片的所有可能情况数
从$n$个不同元素中取出$m$个元素的组合数记为$C_{n}^m$,其计算公式为$C_{n}^m=\frac{n!}{m!(n - m)!}$。
从$4$张卡片中任取$2$张卡片的组合数为$C_{4}^2=\frac{4!}{2!(4 - 2)!}=\frac{4×3×2×1}{(2×1)×(2×1)} = 6$种。
也可以通过列举法得到所有可能情况:$(-2,\sqrt{3})$、$(-2,\frac{5}{7})$、$(-2,\pi)$、$(\sqrt{3},\frac{5}{7})$、$(\sqrt{3},\pi)$、$(\frac{5}{7},\pi)$。
步骤二:找出$2$张卡片都写有无理数的情况数
无理数,也称为无限不循环小数。在$-2$、$\sqrt{3}$、$\frac{5}{7}$、$\pi$中,$\sqrt{3}$和$\pi$是无理数,$-2$是整数,$\frac{5}{7}$是分数,它们都是有理数。
所以$2$张卡片都写有无理数的情况为$(\sqrt{3},\pi)$,共$1$种。
步骤三:根据古典概型概率公式计算概率
古典概型概率公式为$P(A)=\frac{m}{n}$,其中$P(A)$表示事件$A$发生的概率,$m$表示事件$A$包含的基本事件个数,$n$表示基本事件的总数。
设“$2$张卡片都写有无理数”为事件$A$,由上述计算可知$n = 6$,$m = 1$,则$P(A)=\frac{1}{6}$。
14. 甲、乙两人玩猜数字游戏,先由甲心中任想一个数字,记为$a$,再由乙猜甲刚才所想数字. 把乙所猜数字记为$b$,且$a$、$b$都在数字0、1、2、3中选取,若$a$、$b满足|a - b| \leq 1$,则称甲、乙两人“心有灵犀”,他们“心有灵犀”的概率为
$\frac{5}{8}$(或填0.625)
.
答案:$\frac{5}{8}$(或填0.625)
解析:
首先,甲和乙两人都有4种数字可以选择,所以总的可能情况有$4 × 4 = 16$种。
接下来,我们列举出所有满足$|a - b| \leq 1$的情况:
当$a = 0$时,$b$可以取$0,1$,有2种情况;
当$a = 1$时,$b$可以取$0,1,2$,有3种情况;
当$a = 2$时,$b$可以取$1,2,3$,有3种情况;
当$a = 3$时,$b$可以取$2,3$,有2种情况;
所以,满足条件的情况共有$2 + 3 + 3 + 2 = 10$种。
因此,他们“心有灵犀”的概率为$\frac{10}{16} = \frac{5}{8}$。
15. (8分)班级联欢会上通过抽签的方式选择两位同学分别表演唱歌、朗诵,现有甲、乙两位男生和丙、丁两位女生参加抽签.
(1)男生表演唱歌的概率是
$\frac{1}{2}$
;
(2)请用列表或画树状图的方法求出表演唱歌、朗诵的同学都是女生的概率.
答案:(1) $\frac{1}{2}$
(2) 列表如下:
|唱歌|朗诵|
| ---- | ---- |
|甲|乙|
|甲|丙|
|甲|丁|
|乙|甲|
|乙|丙|
|乙|丁|
|丙|甲|
|丙|乙|
|丙|丁|
|丁|甲|
|丁|乙|
|丁|丙|
共有12种等可能的结果,其中表演唱歌、朗诵的同学都是女生的结果有2种(丙,丁;丁,丙),所以概率为$\frac{2}{12}=\frac{1}{6}$。