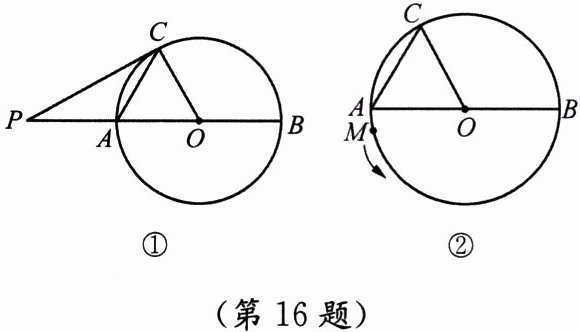
16. (14分)如图①,在⊙O中,AB为⊙O的直径,AC是弦,OC= 4,∠OAC= 60°.
(1) 求∠AOC的度数;
(2) 在图①中,P为直径BA延长线上的一点,当CP与⊙O相切时,求PO的长;
(3) 如图②,一动点M从点A出发,在⊙O上按逆时针方向运动一周,当△MAO的面积与△CAO的面积相等时,求动点M所经过的弧长.
答案:(1) 60°;(2) 8;(3) 4π/3,8π/3,16π/3,20π/3。
解析:
(1) 在△OAC中,OA=OC=4,∠OAC=60°,∴△OAC是等边三角形,∴∠AOC=60°。
(2) ∵CP与⊙O相切,∴OC⊥CP,∠OCP=90°。由(1)知∠AOC=60°,在Rt△OCP中,cos∠COP=OC/PO,∠COP=60°,OC=4,∴PO=OC/cos60°=4/(1/2)=8。
(3) ∵S△MAO=S△CAO=4√3,OA=OM=4,S△MAO=1/2·OA·OM·sin∠AOM=8sin∠AOM,∴sin∠AOM=√3/2,∴∠AOM=60°或120°或240°或300°。弧长l=nπr/180,r=4,∴当n=60°时,l=60π×4/180=4π/3;当n=120°时,l=120π×4/180=8π/3;当n=240°时,l=240π×4/180=16π/3;当n=300°时,l=300π×4/180=20π/3。