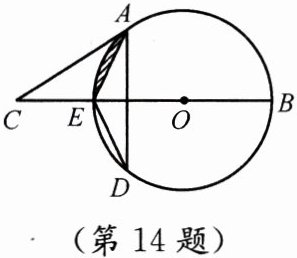
14. (14分)如图,BE是⊙O的直径,A、D是⊙O上的两点,连接AE、AD、DE,过点A作射线交BE的延长线于点C,使∠EAC= ∠EDA.
(1) 求证:AC是⊙O的切线;
(2) 若CE= AE= 2√{3},求阴影部分的面积.
答案:(1) 证明见上;(2) 2π-3√3。
解析:
(1) 连接OA,
∵BE是⊙O直径,∴∠BAE=90°(直径所对圆周角是直角)。
∵∠EDA与∠ABE均为弧AE所对圆周角,∴∠EDA=∠ABE。
∵∠EAC=∠EDA,∴∠EAC=∠ABE。
∵OA=OB,∴∠OAB=∠ABE=∠EAC。
∵∠BAE=∠OAB+∠OAE=90°,∴∠OAC=∠OAE+∠EAC=∠OAE+∠OAB=90°。
∴OA⊥AC,又OA为半径,∴AC是⊙O的切线。
(2) 设⊙O半径为r,则OA=OE=r,OC=OE+CE=r+2√3。
∵AE=CE=2√3,∴△ACE为等腰三角形,∠EAC=∠ECA。
由(1)知∠EAC=∠ABE=α,则∠ECA=α。
在Rt△ABE中,∠BAE=90°,∠ABE=α,∴∠AEB=90°-α。
∵∠AEB+∠AEC=180°(邻补角),∠AEC=180°-2α,
∴(90°-α)+(180°-2α)=180°,解得α=30°。
∴∠AEB=60°,∵OA=OE,∴△OAE为等边三角形,∠AOE=60°,r=AE=2√3。
扇形OAE面积:(60/360)πr²=(1/6)π(2√3)²=2π。
△OAE面积:(√3/4)r²=(√3/4)(2√3)²=3√3。
阴影部分面积=扇形OAE面积-△OAE面积=2π-3√3。
15. (12分)如图,在Rt△ABC中,∠ACB= 90°,以AC为直径作⊙O交AB于点D,连接CD.
(1) 求证:∠A= ∠BCD.
(2) 若M是线段BC上的一点,试问当点M在什么位置时,直线DM与⊙O相切?说明理由.

答案:(1)证明:∵AC为⊙O直径,∴∠ADC=90°(直径所对圆周角为直角)。
在Rt△ABC中,∠ACB=90°,∴∠A+∠B=90°。
在Rt△BDC中,∠BDC=90°(∠ADC=90°),∴∠BCD+∠B=90°。
∴∠A=∠BCD(同角的余角相等)。
(2)当M为BC中点时,DM与⊙O相切。
理由:连接OD。
∵AC为⊙O直径,O为AC中点,∴OA=OD,∠A=∠ADO(等边对等角)。
若DM与⊙O相切,则OD⊥DM(切线垂直于过切点的半径),即∠ODM=90°。
∵∠ADC=90°,∴∠ADO+∠ODC=90°。
又∠ODM=90°,即∠ODC+∠CDM=90°,∴∠ADO=∠CDM。
由(1)知∠A=∠BCD,又∠A=∠ADO,∴∠CDM=∠BCD。
∴△CDM中,CM=DM(等角对等边)。
在Rt△BDC中,M为BC中点时,CM=DM(直角三角形斜边中线等于斜边一半)。
∴当M为BC中点时,DM与⊙O相切。