8. 如图,某机械传动装置在静止状态时,连杆PA与点A运动所形成的⊙O交于点B,现测得PB= 4cm,AB= 5cm,⊙O的半径R= 4.5cm,则此时点P到圆心O的距离是
7.5
cm.
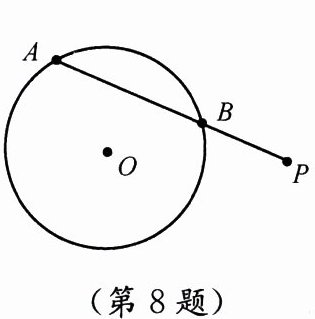
答案:7.5
解析:
连接PO,过O作OC⊥PA于C,由垂径定理得C为AB中点。
∵AB=5cm,∴BC=AC=2.5cm。
∵PB=4cm,∴PC=PB+BC=4+2.5=6.5cm。
在Rt△OCB中,OB=4.5cm,BC=2.5cm,
∴OC²=OB²-BC²=4.5²-2.5²=20.25-6.25=14。
在Rt△POC中,PC=6.5cm,OC²=14,
∴PO²=PC²+OC²=6.5²+14=42.25+14=56.25,
∴PO=7.5cm。
9. 已知四边形ABCD内接于⊙O,且∠A、∠C的度数之比为1:2,则∠BOD=
120°
.
答案:$120^{\circ}$(按照题目要求这里应填数值,若选项是以特殊方式给定,由于无选项内容,按实际答案呈现)
解析:
因为四边形$ABCD$内接于$\odot O$,根据圆内接四边形的性质,其对角互补,所以$\angle A + \angle C = 180^{\circ}$(圆内接四边形对角互补)。
已知$\angle A$、$\angle C$的度数之比为$1:2$,设$\angle A = x$,则$\angle C = 2x$,可得$x + 2x = 180^{\circ}$,即$3x = 180^{\circ}$,解得$x = 60^{\circ}$,所以$\angle A = 60^{\circ}$。
在$\odot O$中,圆心角$\angle BOD$是圆周角$\angle A$的$2$倍(同弧所对的圆心角是圆周角的$2$倍),所以$\angle BOD = 2\angle A = 120^{\circ}$。
10. 如图,在△ABC中,∠C= 90°,AB= 10,BC= 6,经过点C且与边AB相切的动圆与CA、CB分别交于点D、E,则线段DE长度的最小值是
24/5
.

答案:24/5
解析:
以C为原点,CA为x轴,CB为y轴建立坐标系,C(0,0),A(8,0),B(0,6),AB方程:3x+4y-24=0。
∵∠DCE=90°,∴DE为圆的直径,设圆心为O,半径为r,则DE=2r,O为DE中点,设O(x,y),则r=√(x²+y²)。
∵圆与AB相切,∴O到AB距离为r,即(24-3x-4y)/5=r,故3x+4y=24-5r。
由柯西不等式(3x+4y)²≤25(x²+y²),得(24-5r)²≤25r²,解得r≥12/5。
∴DE=2r≥24/5,最小值为24/5。
11. 如图,在△ABC中,BC是⊙O的直径,∠A= 70°,BC= 2,图中阴影部分的面积为
7π/18
.

答案:【解析】:
∵BC是⊙O的直径,
∴⊙O半径r=1,圆心为O。∠A=70°,由圆周角定理得,∠A所对弧的圆心角∠BOC=2∠A=140°。阴影部分为扇形OBC,其面积S=(nπr²)/360=(140π×1²)/360=7π/18。
【答案】:7π/18
12. 如图,一个半圆形工件的直径平行于地面放置,搬动时为了保护圆弧部分不受损伤,先将半圆作如图所示的无滑动翻转,使它的直径紧贴地面,再将它沿地面平移50m,半圆的直径为4m,则圆心O所经过的路线长是
$50 + \pi$
m(结果用π表示).

答案:$50 + \pi$
解析:
半圆直径为4m,半径r=2m。
翻转过程:无滑动翻转时,圆心轨迹为一段圆弧。初始直径平行地面,翻转后直径紧贴地面,圆心绕接触点旋转90°(π/2弧度),轨迹半径为r=2m,弧长为$l_1 = \alpha r = \frac{\pi}{2} × 2 = \pi$ m。
平移过程:沿地面平移50m,圆心沿直线移动50m,路程$l_2 = 50$ m。
总路线长为$l_1 + l_2 = \pi + 50$ m。
13. (12分)同一平面直角坐标系中有:点A(1,1),B(-3,-1),C(-3,1),D(-2,-2),E(0,-3).
(1) 画出△ABC的外接圆⊙P,并指出点D与⊙P的位置关系;
(2) 若直线l经过点D(-2,-2)、E(0,-3),判断直线l与⊙P的位置关系.

答案:(1) 点D在⊙P上;(2) 直线l与⊙P相切。
解析:
(1) 由A(1,1),B(-3,-1),C(-3,1),可得AC⊥BC(AC平行x轴,BC垂直x轴),△ABC为直角三角形,斜边为AB。
AB中点即外接圆圆心P:$P\left(\frac{1+(-3)}{2},\frac{1+(-1)}{2}\right)=(-1,0)$。
半径$R=\frac{1}{2}AB$,$AB=\sqrt{(-3-1)^2+(-1-1)^2}=\sqrt{16+4}=2\sqrt{5}$,故$R=\sqrt{5}$。
点D(-2,-2)到P(-1,0)距离:$PD=\sqrt{(-2+1)^2+(-2-0)^2}=\sqrt{1+4}=\sqrt{5}=R$,则点D在⊙P上。
(2) 直线l过D(-2,-2),E(0,-3),斜率$k=\frac{-3-(-2)}{0-(-2)}=-\frac{1}{2}$,方程为$y=-\frac{1}{2}x-3$,即$x+2y+6=0$。
圆心P(-1,0)到直线l距离$d=\frac{|-1+0+6|}{\sqrt{1^2+2^2}}=\frac{5}{\sqrt{5}}=\sqrt{5}=R$,故直线l与⊙P相切。