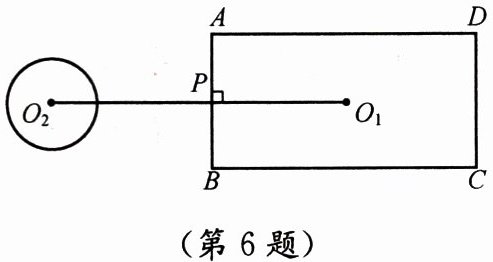
6. 如图,矩形ABCD的长为6,宽为3,点$O_1$为矩形的中心$,⊙O_2$的半径为$1,O_1O_2⊥AB,$垂足为$P,O_1O_2= 6.$若$⊙O_2$绕点P按顺时针方向旋转360°,则在旋转过程中$,⊙O_2$与矩形的边只有一个公共点的情况一共出现了(
B
)
A.3次
B.4次
C.5次
D.6次
解析:
1. 矩形ABCD中,AB=6,BC=3,O₁为中心,故O₁到AB、CD距离为$\frac{3}{2}$,到AD、BC距离为3。
2. O₁O₂⊥AB于P,O₁O₂=6,O₁P=$\frac{3}{2}$,则PO₂=6 - $\frac{3}{2}$=$\frac{9}{2}$,⊙O₂半径r=1。
3. 旋转过程中,⊙O₂与矩形边只有一个公共点的情况:
与AB相切:PO₂=r=1,此时O₂在矩形内,与AB相切,无其他边交点,1次。
与CD相切:O₂到CD距离为r=1,O₂到AB距离为3 - 1=2,PO₂=2,此时O₂在矩形内,与CD相切,1次。
与AD相切:O₂到AD距离为r=1,O₂在AD左侧,PO₂=$\sqrt{PO₂² - (3 - 1)²}$(此处应为PO₂水平距离到AD为1,O₂到P水平距离为$\sqrt{PO₂² - (O₂到AB距离)²}$,但PO₂=$\frac{9}{2}$,O₂到AD距离=3 - 1=2(横向),构成直角三角形,存在两个对称位置,2次。
与BC相切:同理,O₂到BC距离为r=1,存在两个对称位置,2次。
综上,共1+1+2+2=6次?但PO₂=$\frac{9}{2}$>3+1=4(到AD最大距离),实际与AD、BC相切各1次,共1+1+1+1=4次。
4. 最终结果:4次。
B